Special linear group
of degree (order)  over a ring
over a ring 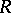
The subgroup 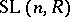 of the general linear group
of the general linear group 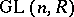 which is the kernel of a determinant homomorphism
which is the kernel of a determinant homomorphism 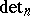 . The structure of
. The structure of 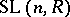 depends on
depends on 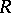 ,
,  and the type of determinant defined on
and the type of determinant defined on 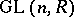 . There are three main types of determinants of importance here: the ordinary determinant in the case when
. There are three main types of determinants of importance here: the ordinary determinant in the case when 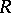 is a commutative ring, the non-commutative Dieudonné determinant (cf. Determinant) when
is a commutative ring, the non-commutative Dieudonné determinant (cf. Determinant) when 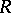 is a division ring (see [1]), and the reduced norm homomorphism for a division ring
is a division ring (see [1]), and the reduced norm homomorphism for a division ring  that is finite dimensional over its centre (see [2]).
that is finite dimensional over its centre (see [2]).
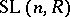 has the following noteworthy subgroups: the group
has the following noteworthy subgroups: the group 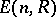 generated by the elementary matrices
generated by the elementary matrices 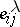 (see Algebraic
(see Algebraic 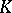 -theory) and, for every two-sided ideal
-theory) and, for every two-sided ideal 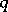 of
of  , the congruence subgroup
, the congruence subgroup 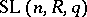 and the group
and the group 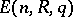 which is the normal subgroup of
which is the normal subgroup of 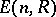 generated by the matrices
generated by the matrices 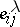 for
for 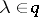 . Let
. Let 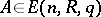 and let
and let
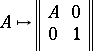 |
be the imbedding of 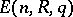 into
into 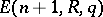 . Then passage to the direct limit gives the group
. Then passage to the direct limit gives the group 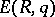 . The group
. The group 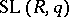 is defined in a similar way. When
is defined in a similar way. When 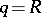 one writes
one writes 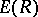 and
and 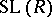 instead of
instead of 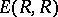 and
and 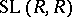 , respectively. The latter is called the stable special linear group of the ring
, respectively. The latter is called the stable special linear group of the ring 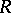 . The normal subgroup structure of
. The normal subgroup structure of 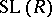 is closely connected with the structure of the groups
is closely connected with the structure of the groups 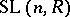 : A subgroup
: A subgroup 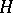 is normal in
is normal in 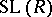 if and only if, for some (unique) two-sided ideal
if and only if, for some (unique) two-sided ideal 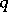 of
of 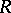 , the following inclusions hold:
, the following inclusions hold:
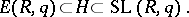 |
Thus, the Abelian groups 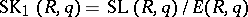 classify the normal subgroups of
classify the normal subgroups of  . The group
. The group 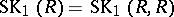 is called the reduced Whitehead group of
is called the reduced Whitehead group of 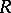 . A satisfactory description of the normal subgroup structure of
. A satisfactory description of the normal subgroup structure of 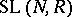 for an arbitrary ring
for an arbitrary ring 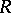 uses a condition involving the stable rank of the ideal
uses a condition involving the stable rank of the ideal 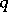 (
(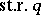 ). Namely, if
). Namely, if  , then there is an isomorphism
, then there is an isomorphism
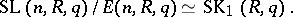 |
In addition, if the conditions 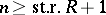 ,
, 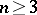 hold, then for every normal subgroup
hold, then for every normal subgroup 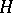 of
of 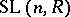 the inclusions
the inclusions
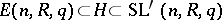 |
hold for an appropriate 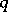 , where
, where 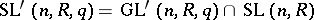 , and
, and 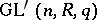 is the pre-image of the centre of
is the pre-image of the centre of 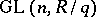 in
in 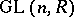 . For certain special rings definitive results are known (see [2], [4], for example).
. For certain special rings definitive results are known (see [2], [4], for example).
In the case of the non-commutative Dieudonné determinant (so that 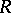 is a division ring), the results are exhaustive. The groups
is a division ring), the results are exhaustive. The groups 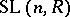 and
and 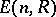 coincide.
coincide. 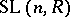 is the commutator subgroup of
is the commutator subgroup of 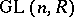 , except in the case of
, except in the case of 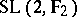 (where
(where 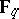 denotes the field of
denotes the field of 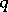 elements). The centre
elements). The centre 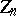 of
of 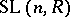 consists of the scalar matrices
consists of the scalar matrices 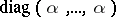 , where
, where 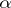 is an element of the centre of
is an element of the centre of 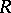 and
and 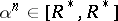 ,
, 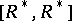 being the commutator subgroup of the multiplicative group
being the commutator subgroup of the multiplicative group 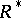 of the division ring
of the division ring 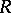 . The quotient group
. The quotient group 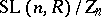 is simple except when
is simple except when 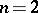 and
and 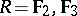 . When
. When 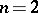 ,
, 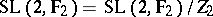 and
and 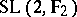 is isomorphic to the symmetric group
is isomorphic to the symmetric group 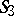 of degree 3, while
of degree 3, while 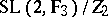 is isomorphic to the alternating group
is isomorphic to the alternating group 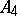 of degree 4.
of degree 4.
If  is a reduced norm homomorphism, then
is a reduced norm homomorphism, then
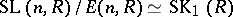 |
and
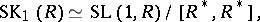 |
so that the group 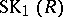 is trivial when
is trivial when 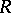 is a field. The conjecture that
is a field. The conjecture that 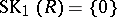 for any division ring
for any division ring 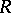 stood for a long time. However, in 1975 it was shown that this is not true (see [5]). The groups
stood for a long time. However, in 1975 it was shown that this is not true (see [5]). The groups 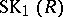 play an important role in algebraic geometry (see [6], [7]). There are also generalizations of the reduced norm homomorphism, which have stimulated a series of new investigations into special linear groups.
play an important role in algebraic geometry (see [6], [7]). There are also generalizations of the reduced norm homomorphism, which have stimulated a series of new investigations into special linear groups.
References
| [1] | E. Artin, "Geometric algebra" , Interscience (1957) |
| [2] | H. Bass, "Algebraic  -theory" , Benjamin (1968) -theory" , Benjamin (1968) |
| [3] | J.W. Milnor, "Introduction to algebraic  -theory" , Princeton Univ. Press (1971) -theory" , Princeton Univ. Press (1971) |
| [4] | A.A. Suslin, "On the structure of the special linear group over polynomial rings" Math. USSR Izv. , 11 (1977) pp. 211–238 Izv. Akad. Nauk SSSR Ser. Mat. , 41 : 2 (1977) pp. 235–252 |
| [5] | V.P. Platonov, "A problem of Tannaka–Artin and groups of projective conorms" Soviet Math. Dokl. , 16 (1975) pp. 781–786 Dokl. Akad. Nauk SSSR , 222 : 2 (1975) pp. 1299–1302 |
| [6] | V.P. Platonov, "The Tannaka–Artin problem and reduced  -theory" Math. USSR Izv. , 10 (1976) pp. 211–243 Izv. Akad. Nauk SSSR Ser. Mat. , 40 : 2 (1976) pp. 227–261 -theory" Math. USSR Izv. , 10 (1976) pp. 211–243 Izv. Akad. Nauk SSSR Ser. Mat. , 40 : 2 (1976) pp. 227–261 |
| [7] | V.P. Platonov, "Algebraic groups and reduced 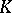 -theory" , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , 1 , Acad. Sci. Fennicae (1980) pp. 311–323 -theory" , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , 1 , Acad. Sci. Fennicae (1980) pp. 311–323 |
Comments
For the reduced norm homomorphism see Reduced norm.
References
| [a1] | A.J. Hahn, O.T. O'Meara, "The classical groups and 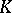 -theory" , Springer (1989) -theory" , Springer (1989) |
Special linear group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Special_linear_group&oldid=18074