Semi-ordered space
A common name for vector spaces on which there is defined a binary partial order relation that is compatible in a certain way with the vector space structure (cf. Vector space). The introduction of an order in function spaces makes it possible to study within the framework of functional analysis problems that are essentially connected with inequalities between functions. However, in contrast to the set of real numbers, which is totally ordered, the natural order in function spaces is only partial; for example, in the space 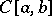 it is natural to say that a function
it is natural to say that a function  majorizes a function
majorizes a function 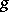 if
if 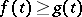 for all
for all 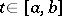 . Under this definition of order, many functions are incomparable with each other.
. Under this definition of order, many functions are incomparable with each other.
Ordered vector spaces.
A vector space 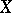 over the field of real numbers is called ordered if there is defined on it a binary order relation
over the field of real numbers is called ordered if there is defined on it a binary order relation 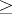 , where
, where 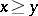 implies
implies 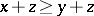 for any
for any 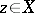 and
and 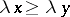 for any number
for any number 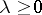 . An example is
. An example is 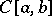 with the natural order. If
with the natural order. If 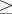 is an order, then the set
is an order, then the set  is a cone, called the positive cone. Conversely, if in a certain space
is a cone, called the positive cone. Conversely, if in a certain space 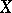 a cone
a cone 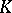 with vertex at the origin is given, then
with vertex at the origin is given, then  can be given an order under which
can be given an order under which 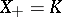 : one should put
: one should put 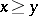 if
if  . One considers also more general ordered vector spaces, in which only a quasi-order structure is defined. In this case
. One considers also more general ordered vector spaces, in which only a quasi-order structure is defined. In this case 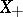 is a wedge, and every wedge with vertex at the origin generates a quasi-order in
is a wedge, and every wedge with vertex at the origin generates a quasi-order in 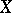 (cf. also Wedge (in a vector space)).
(cf. also Wedge (in a vector space)).
Suppose that a vector space 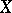 has been provided with an order. The cone
has been provided with an order. The cone 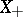 is called generating if
is called generating if 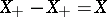 . This property of
. This property of 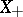 is necessary and sufficient for any finite subset of
is necessary and sufficient for any finite subset of 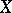 to be bounded (from above and below). The ordered vector spaces in which every set bounded from above has a least upper bound, or supremum, and hence also every set bounded from below has a greatest lower bound, or infimum, are called order complete or (o)-complete. A weaker type of completeness for ordered vector spaces is defined as follows: An ordered vector space is called Dedekind complete if every set which is bounded from above and directed upwards has a least upper bound (a set
to be bounded (from above and below). The ordered vector spaces in which every set bounded from above has a least upper bound, or supremum, and hence also every set bounded from below has a greatest lower bound, or infimum, are called order complete or (o)-complete. A weaker type of completeness for ordered vector spaces is defined as follows: An ordered vector space is called Dedekind complete if every set which is bounded from above and directed upwards has a least upper bound (a set 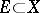 is directed upwards if for any
is directed upwards if for any 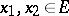 there is an
there is an 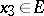 such that
such that 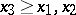 ; cf. also Directed set). If this requirement is satisfied for bounded increasing sequences, then the ordered vector space is called Dedekind (o)-complete. Dedekind completeness is weaker than (o)-completeness. For example, if
; cf. also Directed set). If this requirement is satisfied for bounded increasing sequences, then the ordered vector space is called Dedekind (o)-complete. Dedekind completeness is weaker than (o)-completeness. For example, if  is an arbitrary infinite-dimensional Banach space,
is an arbitrary infinite-dimensional Banach space, 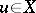 ,
, 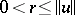 , and if
, and if 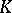 is the cone spanned by the closed ball
is the cone spanned by the closed ball 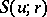 and the element
and the element  , and
, and 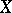 is given the order using
is given the order using 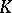 , then
, then  is Dedekind complete but not (o)-complete. An ordered vector space is called Archimedean if the Archimedean axiom holds in it. In particular, every Dedekind (o)-complete ordered vector space is Archimedean.
is Dedekind complete but not (o)-complete. An ordered vector space is called Archimedean if the Archimedean axiom holds in it. In particular, every Dedekind (o)-complete ordered vector space is Archimedean.
One introduces in an ordered vector space the notion of order convergence: A sequence 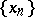 (o)-converges to an element
(o)-converges to an element 
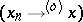 if there are increasing and decreasing sequences
if there are increasing and decreasing sequences 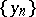 and
and 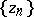 for which
for which  and
and 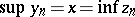 . The (o)-limit has many of the properties of the limit in the set of real numbers, although some of these hold only in Archimedean ordered vector spaces.
. The (o)-limit has many of the properties of the limit in the set of real numbers, although some of these hold only in Archimedean ordered vector spaces.
A linear operator 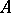 mapping the ordered vector space
mapping the ordered vector space 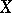 to an ordered vector space
to an ordered vector space 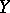 (in particular, a real-valued linear functional) is called positive if
(in particular, a real-valued linear functional) is called positive if 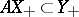 . For positive functionals there is the following theorem on extensions. Let
. For positive functionals there is the following theorem on extensions. Let 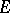 be a linear subset of
be a linear subset of  which majorizes the cone
which majorizes the cone 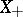 (this means that for any
(this means that for any 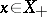 there is a
there is a 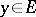 with
with 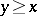 ). Then every linear functional given on
). Then every linear functional given on 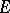 and positive with respect to the cone
and positive with respect to the cone 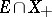 admits a linear positive extension to all of
admits a linear positive extension to all of 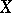 .
.
Vector lattices.
A vector lattice is an ordered vector space in which the order relation defines a lattice structure. Here, for the definition of a vector lattice it suffices to postulate the existence of one of the bounds: the upper 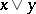 or the lower
or the lower 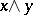 , for any two elements
, for any two elements  of the space. For example, if
of the space. For example, if  exists, then
exists, then 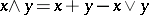 . If
. If 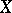 is a vector lattice, then the cone
is a vector lattice, then the cone 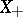 is called minihedral. In a vector lattice, for any element
is called minihedral. In a vector lattice, for any element  its positive and negative parts exist:
its positive and negative parts exist: 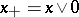 and
and 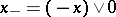 . Here
. Here 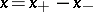 , and this formula gives the "minimal" representation of
, and this formula gives the "minimal" representation of  as a difference of positive elements, that is, if
as a difference of positive elements, that is, if 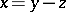 , where
, where 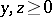 , then
, then 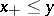 ,
,  . A minihedral cone is generating. The element
. A minihedral cone is generating. The element 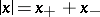 is called the modulus of the element
is called the modulus of the element  . In the space
. In the space 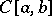 with the natural order, the positive cone is minihedral, the positive part of any function
with the natural order, the positive cone is minihedral, the positive part of any function 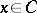 is obtained from
is obtained from  by replacing its negative values by zero, while the modulus is the function
by replacing its negative values by zero, while the modulus is the function 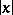 . In a vector lattice, every finite set of elements has upper and lower bounds. The modulus of an element in a vector lattice has many of the properties of the absolute value of a real number.
. In a vector lattice, every finite set of elements has upper and lower bounds. The modulus of an element in a vector lattice has many of the properties of the absolute value of a real number.
The lattice of a vector lattice is distributive. In fact, it satisfies the stronger condition: For an arbitrary set of its elements 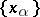 for which
for which 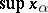 exists, the following formula holds for any
exists, the following formula holds for any 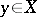 :
: 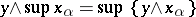 . Then the dual formula
. Then the dual formula 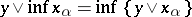 also holds (cf. also Distributive lattice).
also holds (cf. also Distributive lattice).
The theorem on the double partition of positive elements follows: If 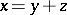 , where
, where 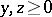 , and simultaneously
, and simultaneously 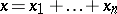 , where all the
, where all the 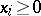 , then every
, then every 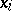 can be represented as
can be represented as 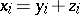 in such a way that
in such a way that 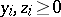 and
and
 |
Two elements 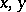 in a vector lattice are called disjoint
in a vector lattice are called disjoint 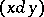 if
if 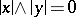 . Two sets
. Two sets 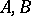 are called disjoint if
are called disjoint if 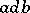 for any
for any 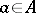 ,
, 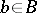 . In the space
. In the space 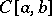 the disjointness
the disjointness 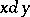 means that
means that 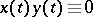 . A positive element
. A positive element  is called a weak unit (a unit in the sense of Freudenthal) if 0 is the only element disjoint to
is called a weak unit (a unit in the sense of Freudenthal) if 0 is the only element disjoint to  . In
. In 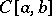 , any function which is greater than 0 on an everywhere-dense set is a weak unit. However, if an element
, any function which is greater than 0 on an everywhere-dense set is a weak unit. However, if an element  is such that for any
is such that for any  there exists a
there exists a 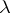 for which
for which 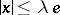 , then
, then  is called a strong unit, and an
is called a strong unit, and an 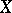 with a strong unit is called a vector lattice of bounded elements. In
with a strong unit is called a vector lattice of bounded elements. In 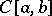 , any function for which
, any function for which 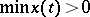 is a strong unit. If in an Archimedean vector lattice
is a strong unit. If in an Archimedean vector lattice 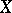 with a strong unit
with a strong unit  one puts
one puts 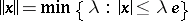 , then
, then 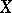 becomes a normed lattice.
becomes a normed lattice.
In the plane, any cone, apart from a one-dimensional cone (that is, a ray), is minihedral. However, in higher-dimensional spaces there are many non-minihedral closed cones, for example all "circular" cones in  . For a cone (with vertex at zero) in an
. For a cone (with vertex at zero) in an  -dimensional Archimedean ordered vector space to be minihedral it is necessary and sufficient that it should be spanned by an
-dimensional Archimedean ordered vector space to be minihedral it is necessary and sufficient that it should be spanned by an 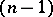 -dimensional simplex with linearly independent vertices. Every Archimedean
-dimensional simplex with linearly independent vertices. Every Archimedean  -dimensional vector lattice is isomorphic to the space
-dimensional vector lattice is isomorphic to the space 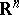 with the coordinatewise ordering.
with the coordinatewise ordering.
 -spaces.
-spaces.
Also called Kantorovich spaces. These are (o)-complete vector lattices. This is the main class of semi-ordered spaces; they are always Archimedean. The notion of (o)-convergence in a 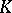 -space is described in terms of upper and lower limits; namely, for a bounded sequence
-space is described in terms of upper and lower limits; namely, for a bounded sequence 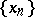 ,
,
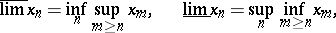 |
and then 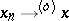 means that
means that 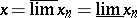 . Let
. Let 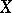 be a
be a 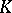 -space. For any set
-space. For any set 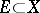 , the set
, the set 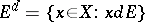 is called its disjoint complement. A set which is the disjoint complement of another set is called a band. For any set
is called its disjoint complement. A set which is the disjoint complement of another set is called a band. For any set 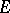 there is a smallest band containing
there is a smallest band containing 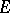 , namely
, namely  ; it is called the band generated by the set
; it is called the band generated by the set 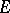 . If
. If 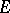 itself is a band, then
itself is a band, then 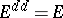 . The band generated by a singleton set is called principal. The notion of a band is also introduced in any vector lattice; however, in a
. The band generated by a singleton set is called principal. The notion of a band is also introduced in any vector lattice; however, in a 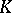 -space it plays a special role, since one has the following theorem on projecting onto a band: If
-space it plays a special role, since one has the following theorem on projecting onto a band: If 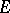 is a band in
is a band in 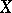 , then for any
, then for any 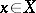 there exists a unique decomposition
there exists a unique decomposition 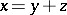 , where
, where 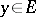 ,
, 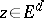 . The linear operator
. The linear operator 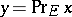 defined here is called projection onto the band
defined here is called projection onto the band 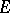 . If one is given an arbitrary collection of pairwise disjoint bands
. If one is given an arbitrary collection of pairwise disjoint bands 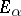 , complete in the sense that 0 is the only element of
, complete in the sense that 0 is the only element of 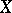 disjoint from all the
disjoint from all the 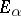 , then any
, then any 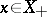 can be written as
can be written as 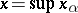 , where
, where 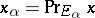 . Every lattice-ideal (
. Every lattice-ideal (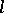 -ideal)
-ideal) 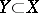 is also a
is also a 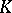 -space. However, if
-space. However, if 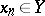 and
and 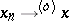 in
in 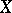 , then this relation also holds in
, then this relation also holds in 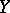 only in the case when the sequence
only in the case when the sequence 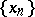 is bounded in
is bounded in 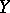 .
.
An example of a 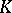 -space is the space
-space is the space 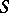 of all real-valued almost-everywhere finite measurable functions on
of all real-valued almost-everywhere finite measurable functions on 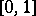 , in which equivalent functions are identified. A function
, in which equivalent functions are identified. A function 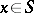 is assumed to be positive if
is assumed to be positive if 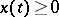 almost-everywhere. If
almost-everywhere. If 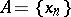 is a countable subset of
is a countable subset of  that is bounded from above (being bounded from above means that there is a
that is bounded from above (being bounded from above means that there is a 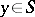 such that
such that 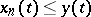 almost-everywhere for any
almost-everywhere for any  ), then the function
), then the function 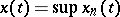 will be the least upper bound of the set
will be the least upper bound of the set 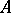 , that is,
, that is, 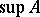 can be computed pointwise. However, for uncountable sets, the calculation of bounds in this way is already impossible, and for uncountable sets it is more difficult to establish the existence of least upper bounds in
can be computed pointwise. However, for uncountable sets, the calculation of bounds in this way is already impossible, and for uncountable sets it is more difficult to establish the existence of least upper bounds in 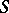 . In
. In 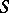 , (o)-convergence means convergence almost-everywhere. All the spaces
, (o)-convergence means convergence almost-everywhere. All the spaces 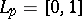 ,
, 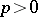 , are lattice-ideals in
, are lattice-ideals in 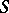 , and hence are also
, and hence are also 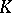 -spaces.
-spaces.
An important role is played by the Riesz–Kantorovich theorem, stating that the set of all order-bounded operators (that is, linear operators taking order-bounded sets to order-bounded sets) from a vector lattice into a  -space with the natural order (
-space with the natural order ( means that
means that 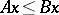 for all
for all 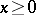 ) is itself a
) is itself a 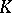 -space. The theory of
-space. The theory of 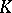 -spaces has found applications in convex analysis and in the theory of extremum problems. Many results here are based on the Hahn–Banach–Kantorovich theorem on the extension of linear operators with values in a
-spaces has found applications in convex analysis and in the theory of extremum problems. Many results here are based on the Hahn–Banach–Kantorovich theorem on the extension of linear operators with values in a 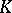 -space.
-space.
A 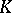 -space is called extended (or laterally complete) if every set of pairwise disjoint elements in it is bounded. An extended
-space is called extended (or laterally complete) if every set of pairwise disjoint elements in it is bounded. An extended 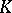 -space always has a weak unit. For any
-space always has a weak unit. For any 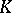 -space
-space 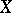 , there exists a unique (up to an isomorphism) extended
, there exists a unique (up to an isomorphism) extended 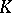 -space
-space 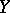 in which
in which 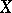 is imbedded as an
is imbedded as an 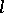 -ideal, and the band in
-ideal, and the band in 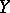 generated by
generated by 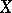 coincides with
coincides with 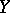 . Such a
. Such a 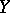 is called the maximal extension of the
is called the maximal extension of the  -space
-space 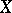 . The space
. The space 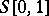 is the maximal extension of all the spaces
is the maximal extension of all the spaces 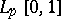 . The notion of an extended
. The notion of an extended 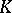 -space plays an important role in the theory of semi-ordered spaces, in particular in representing a
-space plays an important role in the theory of semi-ordered spaces, in particular in representing a  -space by functions.
-space by functions.
Closely associated with a vector lattice and a 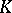 -space is the notion of a lattice-normed space — a vector space to each element of which corresponds its generalized norm, which is an element of a fixed vector lattice and which satisfies the usual norm axioms, in which the inequality sign is understood in the sense of the order of the given vector lattice. Such spaces are used in the theory of functional equations (existence theorems; methods for approximate solution; the Newton–Kantorovich method; monotone processes of successive approximation, etc.).
-space is the notion of a lattice-normed space — a vector space to each element of which corresponds its generalized norm, which is an element of a fixed vector lattice and which satisfies the usual norm axioms, in which the inequality sign is understood in the sense of the order of the given vector lattice. Such spaces are used in the theory of functional equations (existence theorems; methods for approximate solution; the Newton–Kantorovich method; monotone processes of successive approximation, etc.).
Topological semi-ordered spaces.
In functional analysis one also uses ordered vector spaces on which there is also defined a certain topology compatible with the order. The simplest and most important example of such a space is a Banach lattice. A generalization of the concept of a Banach lattice is that of a locally convex lattice.
An important class of Banach 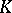 -spaces consists of the Kantorovich–Banach spaces, or
-spaces consists of the Kantorovich–Banach spaces, or 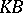 -spaces. This is a Banach
-spaces. This is a Banach 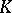 -space satisfying two additional conditions: 1)
-space satisfying two additional conditions: 1) 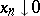 implies
implies 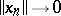 (order-continuity of the norm); 2) if the sequence
(order-continuity of the norm); 2) if the sequence 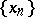 is increasing and not order-bounded, then
is increasing and not order-bounded, then 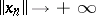 . In
. In  -spaces it is possible to describe in terms of the norm many facts the meaning of which depend only on the order. For example,
-spaces it is possible to describe in terms of the norm many facts the meaning of which depend only on the order. For example,  means that
means that 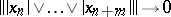 as
as 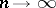 , uniformly with respect to
, uniformly with respect to 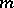 . For a set
. For a set 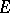 in a
in a 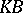 -space to be order-bounded it is necessary and sufficient that the set of all numbers of the form
-space to be order-bounded it is necessary and sufficient that the set of all numbers of the form 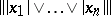 , where
, where 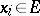 , should be bounded. A
, should be bounded. A 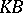 -space is a regular
-space is a regular 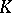 -space.
-space.
An example of a 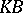 -space:
-space: 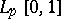 for
for 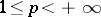 .
.
Let 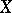 be an arbitrary locally convex space equipped with an ordered vector space structure and having a so-called normal cone
be an arbitrary locally convex space equipped with an ordered vector space structure and having a so-called normal cone 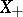 ; here normality of
; here normality of  is equivalent to the supposition that
is equivalent to the supposition that 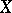 has a base of absolutely-convex and order-saturated neighbourhoods
has a base of absolutely-convex and order-saturated neighbourhoods 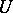 of zero (meaning that if
of zero (meaning that if 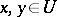 and
and 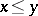 , then also the whole interval
, then also the whole interval 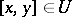 ). For every continuous linear functional on a locally convex ordered vector space to be representable as the difference of positive continuous linear functionals, it is necessary and sufficient that the cone
). For every continuous linear functional on a locally convex ordered vector space to be representable as the difference of positive continuous linear functionals, it is necessary and sufficient that the cone 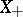 is normal in the weak topology. For normed spaces, normality of the cone in the weak and in the strong topology are equivalent.
is normal in the weak topology. For normed spaces, normality of the cone in the weak and in the strong topology are equivalent.
References
| [1] | B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian) |
| [2] | L.V. Kantorovich, B.Z. Vulikh, A.G. Pinsker, "Functional analysis in semi-ordered spaces" , Moscow-Leningrad (1950) (In Russian) |
| [3] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) |
| [4] | M.A. Krasnosel'skii, "Positive solutions of operator equations" , Wolters-Noordhoff (1964) (Translated from Russian) |
| [5] | M.Ya. Antonovskii, V.G. Boltyanskii, T.A. Sarymsakov, "Topological Boolean algebras" , Tashkent (1963) (In Russian) |
| [6] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [7] | L.V. Kantorovich, G.P. Akilov, "Functional analysis in normed spaces" , Pergamon (1964) (Translated from Russian) |
| [8] | , Functional analysis , Math. Reference Library , Moscow (1972) (In Russian) |
| [9] | B.Z. Vulikh, "Introduction to the theory of cones in normed spaces" , Kalinin (1977) (In Russian) |
| [10] | M.G. Krein, M.A. Rutman, "Linear operators leaving invariant a cone in a Banach space" Transl. Amer. Math. Soc. , 26 (1956) Uspekhi Mat. Nauk , 3 : 1 (1948) pp. 3–95 |
| [11] | A.V. Bukhvalov, A.I. Veksler, G.Ya. Lozanovskii, "Banach lattices - some Banach aspects of their theory" Russian Math. Surveys , 34 : 2 (1979) pp. 159–212 Uspekhi Mat. Nauk , 34 : 2 (1979) pp. 137–183 |
| [12] | G.P. Akilov, S.S. Kutateladze, "Ordered vector spaces" , Novosibirsk (1978) (In Russian) |
Comments
Cf. also Riesz space.
References
| [a1] | H. Freudenthal, "Teilweise geordnete Moduln" Proc. Royal Acad. Sci. Amsterdam , 39 (1936) pp. 641–651 |
| [a2] | H.H. Schaefer, "Banach lattices and positive operators" , Springer (1974) |
| [a3] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971) |
| [a4] | A.C. Zaanen, "Riesz spaces" , II , North-Holland (1982) |
Semi-ordered space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-ordered_space&oldid=18044