Boolean-valued model

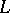A model defined as follows. Let be the signature of some first-order language with one kind of variables, i.e. is the set of symbols of functions and predicates. A Boolean-valued model then is a triple 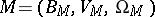, where 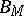is a non-degenerate Boolean algebra, 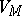is a non-empty set, and 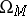is a function defined on such that

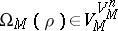if 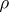is an -place function symbol, and

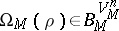if 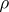is an -place predicate symbol. The symbol 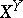denotes the set of all functions defined on 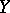with values in 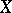and 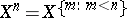, where 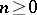is a natural number. The Boolean algebra 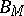is called the set of truth values of the model 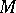. The set 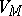is called the universe of 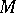. A Boolean-valued model 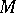is also called a 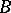-model if the set of truth values is the Boolean algebra 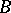, 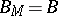. If a Boolean algebra 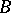is a two-element algebra (i.e. 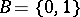), then the 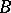-model 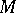is the classical two-valued model.

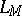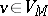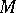Let be a language, complemented by new individual constants: each having its own individual constant . Let be a 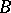-model and let 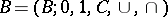be a complete Boolean algebra; the equalities 1)–8) below then define the value 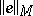of each closed expression (i.e. of a formula or a term without free variables) of :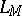

1) 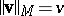, where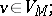

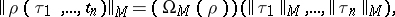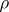2) where are closed terms and is an -place function or predicate symbol;

3)

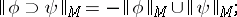
4)

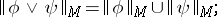
5)

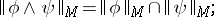
6)

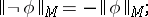
7)

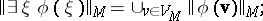
8)

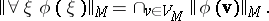
The relations 1)–8) define the value for certain non-complete Boolean algebras as well; the only condition is that the infinite unions and intersections in 7) and 8) exist. The concept of a Boolean-valued model can also be introduced for languages with more than one kind of variables. In such a case each kind of variable has its own domain of variation .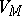

A closed formula 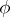is said to be true in a 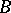-model 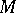(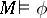) if

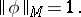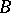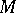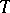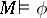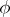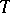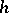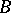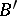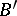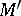A -model is said to be a model of a theory if for all axioms of . If is a homomorphism of a Boolean algebra into a Boolean algebra preserving infinite unions and intersections, then there exists a model such that

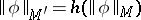for each closed formula 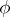of 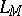. If the universe of a model 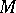is countable, then there exists a homomorphism 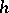into the Boolean algebra 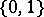, under which 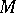is transformed into the classical two-valued model 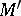such that

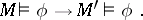It has been shown that a theory 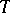is consistent if and only if it has a Boolean-valued model. This theorem forms the basis of the application of the theory of Boolean-valued models to problems of the consistency of axiomatic theories.

If the Boolean-valued model of a theory 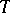is constructed by means of another axiomatic theory 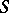, then one obtains the statement on the consistency of 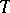relative to 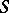. Thus, the result due to P. Cohen on the consistency of the theory 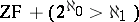relative to ZF is obtained by constructing the respective Boolean-valued model by means of the system ZF (cf. Forcing method). The construction of the Cohen forcing relation 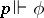is equivalent to that of a Boolean-valued model 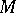such that

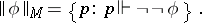References

[1]	E. Rasiowa, R. Sikorski, "The mathematics of metamathematics" , Polska Akad. Nauk (1963)
[2]	T.J. Jech, "Lectures in set theory: with particular emphasis on the method of forcing" , Lect. notes in math. , 217 , Springer (1971)
[3]	G. Takeuti, W.M. Zaring, "Axiomatic set theory" , Springer (1973)
[4]	Yu.I. Manin, "The problem of the continuum" J. Soviet Math. , 5 : 4 (1976) pp. 451–502 Itogi Nauk. i Tekhn. Sovrem. Problemy , 5 (1975) pp. 5–73

References

[a1]	J.L. Bell, "Boolean-valued models and independence proofs in set theory" , Clarendon Press (1977)
[a2]	T.J. Jech, "Set theory" , Acad. Press (1978) (Translated from German)
[a3]	K. Kunen, "Set theory" , North-Holland (1980)