Classifying space

The base 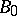of a universal fibre bundle .

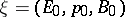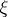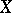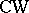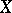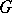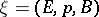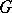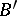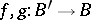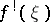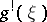The universality of the bundle is to be understood in the following sense. Let be the set of equivalence classes (with respect to a notion of isomorphism (covering the identity mapping of )) of locally trivial bundles over the -complex with structure group . If is a locally trivial bundle with structure group , is a topological space and are homotopic mappings, then the induced bundles and over 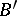belong to the same class in 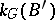. A locally trivial bundle 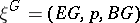is now called universal if the mapping 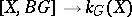, , 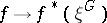is one-to-one (and onto) for any 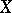. In this case, the space 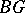is called a classifying space of the group 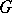. A principal bundle with structure group 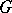is universal (in the class of locally trivial bundles over 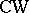-complexes) if the space of the bundle has trivial homotopy groups.

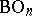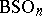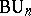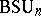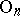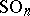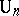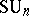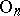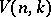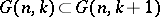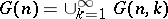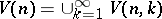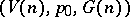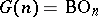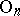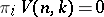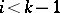The most important examples of classifying spaces are , , , for the respective groups , , , , and are constructed as follows. Let be the Grassmann manifold; it is the base of the principal -bundle with the Stiefel manifold as total space. The natural imbeddings and allow one to form the unions and . The bundle is universal and is a classifying space for the group ( for and 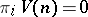for all 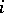). The Grassmann manifold (the space of -dimensional planes with a fixed orientation in 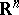) leads in analogous fashion to the classifying space 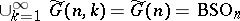for the group 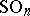. The classifying spaces for the groups 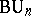and 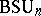are similarly constructed, but with the difference that here complex Grassmann manifolds are considered.

For any 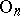-bundle 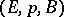(where 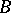is a 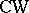-complex) there exists a mapping under which the induced bundle over 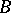is isomorphic to 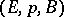. In the case when 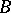is a smooth -dimensional manifold and the principal 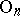-bundle 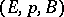is associated with the tangent vector bundle to 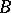, the construction of is especially simple: The manifold 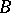is imbedded in a Euclidean space 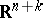for sufficiently large 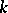and , , 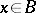is taken to coincide with the -dimensional subspace of 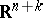obtained by a displacement of the tangent space to 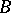at . The Grassmann manifolds provide a convenient method of constructing classifying spaces for vector bundles. There are also constructions enabling one to construct classifying spaces functorially for any topological group. The most commonly used is the Milnor construction 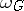(see Principal fibre bundle) for which 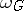is universal in the wider category of all numerable 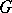-bundles over an arbitrary topological space.

Classifying spaces play an important role for spherical bundles 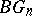over a 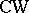-complex 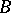; the Milnor construction is not suitable for the construction of the spaces 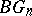(and of 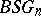for orientable spherical bundles) since the set of homotopy equivalences 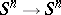is not a group but an 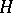-space. An explicit construction of these spaces is given in [2]. There also exist classifying spaces 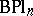and 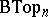for piecewise-linear and topological microbundles.

There is a natural mapping 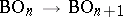corresponding to the addition of a one-dimensional trivial bundle to a vector bundle. The mapping can be regarded as an imbedding, so that it makes sense to consider the union in the inductive limit topology. The spaces 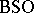, , 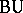, , 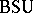, , 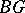, 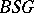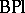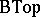etc., are constructed in a completely analogous fashion. These are classifying spaces for stable equivalence classes of bundles given over connected finite 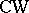-complexes. All these spaces have 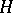-space structures coming from the operation of Whitney sums of fibre bundles.

The term "classifying space" is not used solely in connection with fibre bundles. Sometimes classifying space refers to the representing space (object) for an arbitrary representable functor 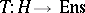of the homotopy category into the category of sets. An example of such a classifying space is the space 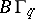which classifies in some sense foliations (cf. Foliation) of codimension 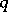on a manifold, or, more generally, Haefliger 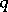-structures on an arbitrary topological space.

References

[1]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)
[2]	J.M. Boardman, R.M. Vogt, "Homotopy invariant algebraic structures on topological spaces" , Springer (1973)

Comments

Two vector bundles 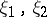are stably equivalent (with respect to some notion of isomorphism) if there are trivial bundles 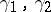such that the Whitney sums (direct sums) 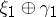and 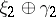are isomorphic in the chosen sense.

An open covering 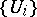of a topological space is numerable if there exists a locally finite partition of unity such that 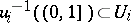for all . A 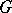-bundle 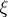over 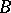is numerable if there is a numerable covering 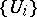such that 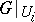is trivial for all .

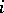Very often in the literature classifying space of a group is defined as the base space of a totally acyclic principal fibre bundle. One may as well (as is done above) consider the class of locally trivial fibre bundles with structure group 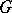, and define a classifying space as the base space of a universal locally trivial bundle. In principle the classifying space thus defined depends then also on the special fibre type. But as it is proved in the literature (up to homotopy equivalence) the classifying spaces are independent of the fibre type.

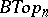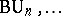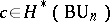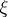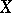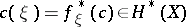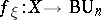For more on such classifying spaces as and cf. [a2]. The elements of the cohomology rings of classifying spaces such as , define characteristic classes (cf. Characteristic class) by assigning e.g. for a given element to an -dimensional complex vector bundle over the cohomology element where is the mapping (unique up to homotopy) such that 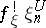is isomorphic to 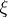(where 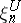is the universal complex vector bundle over 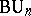); 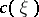is called the characteristic cohomology class of 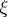determined by .

References

[a1]	J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974)
[a2]	J. Madsen, R.J. Milgram, "The classifying spaces for surgery and cobordism of manifolds" , Princeton Univ. Press (1979)