Theta-function
 -function, of one complex variable
-function, of one complex variable
A quasi-doubly-periodic entire function of a complex variable  , that is, a function
, that is, a function  having, apart from a period
having, apart from a period  , also a quasi-period
, also a quasi-period  ,
,  , the addition of which to the argument multiplies the value of the function by a certain factor. In other words, one has the identities (in
, the addition of which to the argument multiplies the value of the function by a certain factor. In other words, one has the identities (in  ):
):
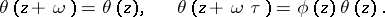 |
As a periodic entire function, a theta-function can always be represented by a series
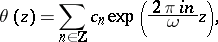 | (1) |
where the coefficients  must be chosen so as to ensure convergence. The series (1) is called a theta-series (because of the original notation). Other representations of theta-functions, for example as infinite products, are also possible.
must be chosen so as to ensure convergence. The series (1) is called a theta-series (because of the original notation). Other representations of theta-functions, for example as infinite products, are also possible.
In applications one usually restricts oneself to multipliers of the form
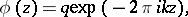 |
where  is a natural number, called the order or the weight of the theta-function, and
is a natural number, called the order or the weight of the theta-function, and  is a number. Convergence is ensured, for example, by using coefficients of the form
is a number. Convergence is ensured, for example, by using coefficients of the form
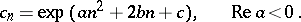 |
In many problems it is convenient to take the theta-functions that satisfy the conditions
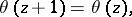 | (2) |
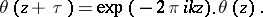 |
All theta-functions of the form (2) of the same order 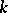 form a vector space of dimension
form a vector space of dimension 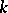 . A basis for this vector space can be written in the form
. A basis for this vector space can be written in the form
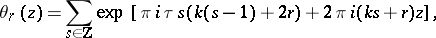 |
 |
Individual examples of theta-functions are already encountered in the work of J. Bernoulli (1713), L. Euler, and in the theory of heat conduction of J. Fourier. C.G.J. Jacobi subjected theta-functions to a systematic investigation, and picked out four special theta-functions, which formed the basis of his theory of elliptic functions (cf. Jacobi elliptic functions).
Theta-functions of several complex variables arise as a natural generalization of theta-functions of one complex variable. They are constructed in the following way. Let  be a row-matrix of
be a row-matrix of 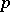 complex variables,
complex variables, 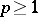 , let
, let 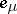 be the
be the  -th row of the identity matrix
-th row of the identity matrix  of order
of order 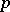 , let
, let 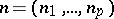 be an integer row-matrix, and let
be an integer row-matrix, and let 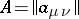 be a symmetric complex matrix of order
be a symmetric complex matrix of order 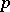 such that the matrix
such that the matrix 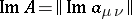 gives rise to a positive-definite quadratic form
gives rise to a positive-definite quadratic form 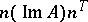 . (Here
. (Here  is the transpose of the matrix
is the transpose of the matrix  .) The multiple theta-series
.) The multiple theta-series
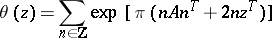 | (3) |
converges absolutely and uniformly on compacta in  , and hence defines an entire transcendental function of
, and hence defines an entire transcendental function of 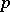 complex variables
complex variables 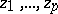 , called a theta-function of order
, called a theta-function of order 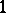 . The individual elements of the matrix
. The individual elements of the matrix 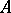 are called moduli, or parameters, of the theta-function
are called moduli, or parameters, of the theta-function  . The number of moduli is equal to
. The number of moduli is equal to  . A theta-function
. A theta-function 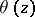 of the first order satisfies the following basic identities (in
of the first order satisfies the following basic identities (in  ):
):
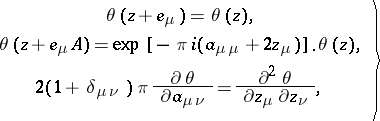 | (4) |
where 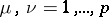 , and
, and 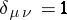 for
for  and
and  for
for  . The
. The 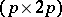 -matrix
-matrix 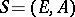 is the moduli system or system of periods and quasi-periods of
is the moduli system or system of periods and quasi-periods of 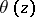 . If
. If  ,
, 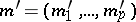 are arbitrary integer row-matrices, then the periodicity property of theta-functions can be written in its most general form as
are arbitrary integer row-matrices, then the periodicity property of theta-functions can be written in its most general form as
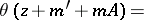 |
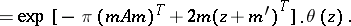 |
Let  ,
,  be arbitrary complex row-matrices, and let
be arbitrary complex row-matrices, and let  be the
be the  -matrix
-matrix
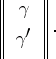 |
Then the formula
 |
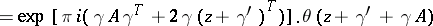 |
defines a theta-function of order 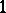 with characteristic (in general form)
with characteristic (in general form) 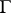 . In this terminology the theta-function (3) has characteristic 0. The matrix
. In this terminology the theta-function (3) has characteristic 0. The matrix  is also called the periodicity characteristic of the matrix
is also called the periodicity characteristic of the matrix 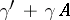 . One always has
. One always has 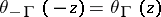 . Property (4) generalizes to theta-functions of characteristic
. Property (4) generalizes to theta-functions of characteristic 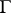 :
:
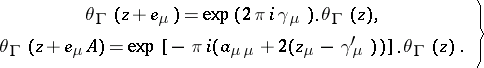 | (5) |
The characteristic is said to be normal if  for
for  .
.
The most commonly used are fractional characteristics, where all the  and
and 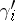 are non-negative proper fractions with common denominator
are non-negative proper fractions with common denominator 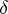 . The simplest and most important case is of semi-integer or half characteristics, where
. The simplest and most important case is of semi-integer or half characteristics, where 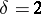 . A semi-integer characteristic
. A semi-integer characteristic
 |
can be thought of as being made up of the numbers 0 and 1 (usually a "theta-characteristictheta-characteristic" is used to mean just such a characteristic). For a theta-function with characteristic 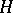 equations (5) take the form
equations (5) take the form
 |
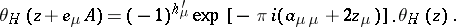 |
A theta-characteristic 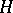 is called even or odd, depending on whether the theta-function
is called even or odd, depending on whether the theta-function 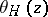 is even or odd. In other words, the theta-characteristic
is even or odd. In other words, the theta-characteristic 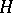 is even or odd, depending on whether the number
is even or odd, depending on whether the number  is even or odd, since
is even or odd, since
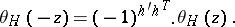 |
There are 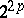 distinct theta-characteristics, of which
distinct theta-characteristics, of which 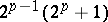 are even and
are even and 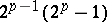 are odd. The theta-function
are odd. The theta-function 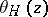 takes the value zero at those points
takes the value zero at those points  whose theta-characteristic
whose theta-characteristic
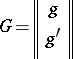 |
yields an odd theta-characteristic when added to 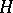 . Jacobi used theta-functions with semi-integer characteristics in his theory of elliptic functions, except that his had period
. Jacobi used theta-functions with semi-integer characteristics in his theory of elliptic functions, except that his had period 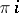 rather than 1.
rather than 1.
Let  be a natural number. An entire transcendental function
be a natural number. An entire transcendental function 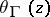 is called a theta-function of order
is called a theta-function of order 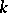 with characteristic
with characteristic  if it satisfies the identities
if it satisfies the identities
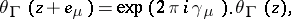 |
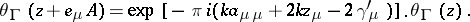 |
For example, the product of 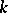 theta-functions of order 1 is a theta-function of order
theta-functions of order 1 is a theta-function of order 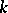 .
.
Using theta-functions of order 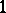 with semi-integer characteristics one can construct meromorphic Abelian functions with
with semi-integer characteristics one can construct meromorphic Abelian functions with 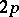 periods. The periods of an arbitrary Abelian function in
periods. The periods of an arbitrary Abelian function in  complex variables satisfy the Riemann–Frobenius relations, which yield convergence for the series defining the theta-functions with the corresponding system of moduli. According to a theorem formulated by K. Weierstrass and proved by H. Poincaré, an Abelian function can be represented as a quotient of entire theta-functions with corresponding moduli system. For the solution of the Jacobi inversion problem on Abelian integrals, one constructs a special Riemann theta-function, whose argument is a system of points
complex variables satisfy the Riemann–Frobenius relations, which yield convergence for the series defining the theta-functions with the corresponding system of moduli. According to a theorem formulated by K. Weierstrass and proved by H. Poincaré, an Abelian function can be represented as a quotient of entire theta-functions with corresponding moduli system. For the solution of the Jacobi inversion problem on Abelian integrals, one constructs a special Riemann theta-function, whose argument is a system of points 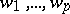 on a Riemann surface.
on a Riemann surface.
See also Theta-series.
References
| [1] | N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) pp. Chapt. 9 (In Russian) |
| [2] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 , Springer (1964) pp. Chapt.8 |
| [3] | A. Krazer, "Lehrbuch der Theta-Funktionen" , Chelsea, reprint (1970) |
| [4] | F. Conforto, "Abelsche Funktionen und algebraische Geometrie" , Springer (1956) |
Comments
The conditions on the matrix  used in the construction of a theta-function in
used in the construction of a theta-function in  variables (3) are precisely those needed in order that the lattice
variables (3) are precisely those needed in order that the lattice 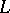 defined by the matrix
defined by the matrix 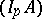 in
in 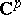 be such that
be such that  be an Abelian variety. All Abelian varieties over
be an Abelian variety. All Abelian varieties over 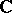 arise this way. Thus, there is a theta-function attached to any Abelian variety.
arise this way. Thus, there is a theta-function attached to any Abelian variety.
In particular, the conditions are satisfied by the canonical period matrix for Abelian differentials of the first kind on a Riemann surface (cf. Abelian differential), thus determining the Jacobi variety of the Riemann surface and an associated theta-function.
For a not necessarily canonical period matrix 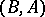 these relations are
these relations are 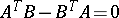 (Riemann's equality, which becomes symmetry for
(Riemann's equality, which becomes symmetry for  in the canonical case when
in the canonical case when 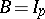 ) and
) and 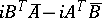 is positive-definite Hermitean (Riemann's inequality, which becomes positive definiteness of the imaginary part of
is positive-definite Hermitean (Riemann's inequality, which becomes positive definiteness of the imaginary part of 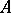 in the canonical case (using the symmetry of
in the canonical case (using the symmetry of 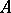 )), [a8], p. 27. Together these two relations are sometimes known as the Riemann bilinear relations.
)), [a8], p. 27. Together these two relations are sometimes known as the Riemann bilinear relations.
References
| [a1] | C.L. Siegel, "Topics in complex function theory" , 2 , Wiley (Interscience) (1971) |
| [a2] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
| [a3] | D. Mumford, "Tata lectures on Theta" , 1–2 , Birkhäuser (1983–1984) |
| [a4] | D. Mumford, "On the equations defining abelian varieties I" Invent. Math. , 1 (1966) pp. 287–354 |
| [a5] | D. Mumford, "On the equations defining abelian varieties II-III" Invent. Math. , 3 (1967) pp. 71–135; 215–244 |
| [a6] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1985) |
| [a7] | J.-i. Igusa, "Theta functions" , Springer (1972) |
| [a8] | R.C. Gunning, "Riemann surfaces and generalized theta functions" , Springer (1976) |
| [a9] | J.D. Fay, "Theta functions on Riemann surfaces" , Springer (1973) |
Theta-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Theta-function&oldid=17955