Euler polynomials
Polynomials of the form
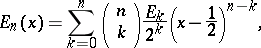 |
where  are the Euler numbers. The Euler polynomials can be computed successively by means of the formula
are the Euler numbers. The Euler polynomials can be computed successively by means of the formula
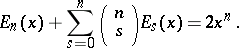 |
In particular,
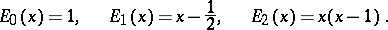 |
The Euler polynomials satisfy the difference equation
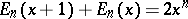 |
and belong to the class of Appell polynomials, that is, they satisfy
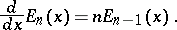 |
The generating function of the Euler polynomials is
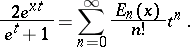 |
The Euler polynomials admit the Fourier expansion
 | (*) |
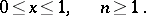 |
They satisfy the relations
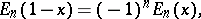 |
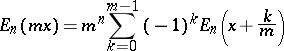 |
if 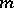 is odd,
is odd,
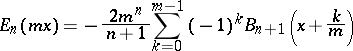 |
if 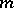 is even. Here
is even. Here  is a Bernoulli polynomial (cf. Bernoulli polynomials). The periodic functions coinciding with the right-hand side of (*) are extremal in the Kolmogorov inequality and in a number of other extremal problems in function theory. Generalized Euler polynomials have also been considered.
is a Bernoulli polynomial (cf. Bernoulli polynomials). The periodic functions coinciding with the right-hand side of (*) are extremal in the Kolmogorov inequality and in a number of other extremal problems in function theory. Generalized Euler polynomials have also been considered.
References
| [1] | L. Euler, "Opera omnia: series prima: opera mathematica: institutiones calculi differentialis" , Teubner (1980) (Translated from Latin) |
| [2] | N.E. Nörlund, "Volesungen über Differenzenrechnung" , Springer (1924) |
Comments
The Euler polynomials satisfy in addition the identities
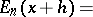 |
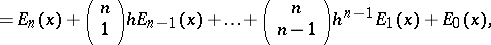 |
written symbolically as
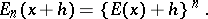 |
Here the right-hand side should be read as follows: first expand the right-hand side into sums of expressions 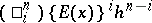 and then replace
and then replace 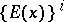 with
with 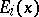 .
.
Using the same symbolic notation one has for every polynomial 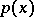 ,
,
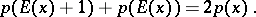 |
Euler polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_polynomials&oldid=17907