Markov moment

Markov time

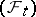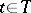A notion used in probability theory for random variables having the property of independence of the "future" . More precisely, let be a measurable space with a non-decreasing family , , of 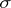-algebras of 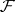( 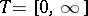in the case of continuous time and 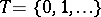in the case of discrete time). A random variable 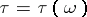with values in 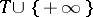is called a Markov moment or Markov time (relative to the family 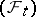, 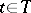) if for each 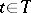the event 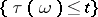belongs to 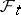. In the case of discrete time this is equivalent to saying that for any 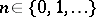the event 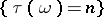belongs to .

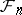Examples.

1) Let 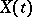, , 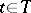be a real-valued right-continuous random process given on 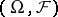, and let 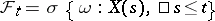. Then the random variables

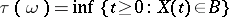and

that is, the (first and first after 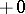) times of hitting the (Borel) set 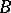, form Markov moments (in the case 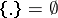it is assumed that ).

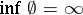2) If , , 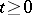is a standard Wiener process, then the Markov moment

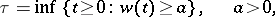has probability density

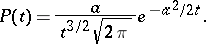Here , but .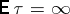

3) The random variable

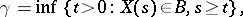being the first time after which remains in 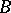, is an example of a non-Markov moment (a random variable depending on the "future" ).

Using the idea of a Markov moment one can formulate the strong Markov property of Markov processes (cf. Markov process). Markov moments and stopping times (that is, finite Markov moments) play a major role in the general theory of random processes and statistical sequential analysis.

References

[1]	I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian)

References

[a1]	R.M. Blumenthal, R.K. Getoor, "Markov processes and potential theory" , Acad. Press (1968)
[a2]	J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390
[a3]	E.B. Dynkin, "Markov processes" , 1 , Springer (1965) (Translated from Russian)
[a4]	A.D. [A.D. Ventsel'] Wentzell, "A course in the theory of stochastic processes" , McGraw-Hill (1981) (Translated from Russian)
[a5]	L.P. Breiman, "Probability" , Addison-Wesley (1968)