Exact sequence
A sequence
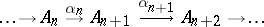 |
of objects of an Abelian category  and of morphisms
and of morphisms  such that
such that
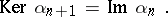 |
An exact sequence 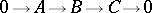 is called short, and consists of an object
is called short, and consists of an object 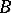 , a subobject
, a subobject 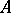 of it and the corresponding quotient object
of it and the corresponding quotient object  .
.
Comments
Exact sequences often occur and are often used in (co)homological considerations. There are, e.g., the long homology exact sequence
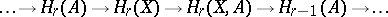 |
of a pair  ,
, 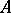 a subspace of
a subspace of 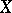 , and the long cohomology exact sequence
, and the long cohomology exact sequence
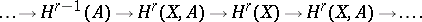 |
Analogous long exact sequences occur in a variety of other homology and cohomology theories. Cf. Homology theory; Cohomology; Cohomology sequence; Homology sequence, and various articles on the (co)homology of various kinds of objects, such as Cohomology of algebras; Cohomology of groups; Cohomology of Lie algebras.
An exact sequence of the form 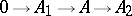 is sometimes called a left short exact sequence and one of the form
is sometimes called a left short exact sequence and one of the form 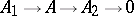 a right short exact sequence. The exact sequence of a morphism
a right short exact sequence. The exact sequence of a morphism  in an Abelian category is the exact sequence
in an Abelian category is the exact sequence
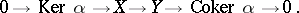 |
Exact sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Exact_sequence&oldid=17886