Conjugate harmonic functions

harmonically-conjugate functions

A pair of real harmonic functions and which are the real and imaginary parts of some analytic function 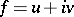of a complex variable. In the case of one complex variable , two harmonic functions 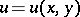and 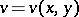are conjugate in a domain 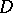of the complex plane 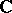if and only if they satisfy the Cauchy–Riemann equations in :

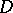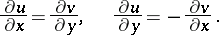(1)

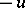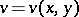The roles of and in (1) are not symmetric: is a conjugate for but , and not , is a conjugate for . Given a harmonic function , a local conjugate and a local complete analytic function 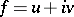are easily determined up to a constant term. This can be done, for example, using the Goursat formula

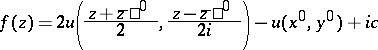(2)

in a neighbourhood of some point in the domain of definition of .

In the case of several complex variables 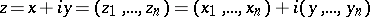, , 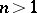the Cauchy–Riemann system becomes overdetermined

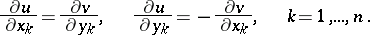(3)

It follows from (3) that for 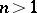, can no longer be taken as an arbitrary harmonic function; it must belong to the subclass of pluriharmonic functions (cf. Pluriharmonic function). The conjugate pluriharmonic function can then be found using (2).

There are various analogues of conjugate harmonic functions 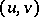involving a vector function 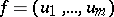whose components 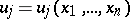are real functions of real variables . An example is a gradient system 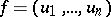satisfying the generalized system of Cauchy–Riemann equations

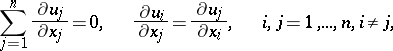(4)

which can also be written in abbreviated form:

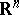If the conditions (4) hold in a domain of a Euclidean space homeomorphic to a ball, then there is a harmonic functi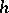on on 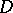such that 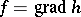. When 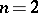, it turns out that 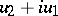is an analytic function of the variable 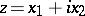. The behaviour of the solutions of (4) is in some respects similar to that of the Cauchy–Riemann system (1), for example in the study of boundary properties (see [3]).

References

[1]	A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian)
[2]	V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian)
[3]	E.M. Stein, G. Weiss, "Introduction to Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971)