Kervaire-Milnor invariant
An invariant of framed surgery of a closed 6- or  -dimensional framed manifold.
-dimensional framed manifold.
Let 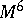 be a stably-parallelizable
be a stably-parallelizable  -connected manifold on which is given a stable
-connected manifold on which is given a stable 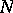 -dimensional framing
-dimensional framing  , i.e. a trivialization of the stable
, i.e. a trivialization of the stable 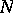 -dimensional normal bundle. Let
-dimensional normal bundle. Let 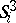 be spheres realizing a basis of the
be spheres realizing a basis of the  -dimensional homology space of
-dimensional homology space of 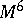 . By summing the given
. By summing the given 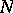 -trivialization
-trivialization 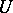 with certain trivializations
with certain trivializations 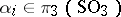 of tubular neighbourhoods of the spheres
of tubular neighbourhoods of the spheres 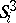 in
in 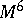 , one obtains an
, one obtains an 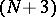 -dimensional trivialization of the stable normal bundles to the spheres
-dimensional trivialization of the stable normal bundles to the spheres  and the corresponding elements
and the corresponding elements 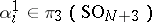 . The cokernel of the stable homomorphism
. The cokernel of the stable homomorphism  is isomorphic to
is isomorphic to 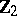 for
for 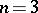 , so that each sphere
, so that each sphere  is put into correspondence with an element of the group
is put into correspondence with an element of the group 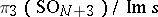 (according to the value of the elements
(according to the value of the elements 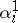 which they take in the group
which they take in the group 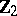 after factorization by
after factorization by 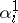 ). This value does not depend on the choice of the elements
). This value does not depend on the choice of the elements 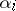 , but depends only on the homology classes realized by the spheres
, but depends only on the homology classes realized by the spheres 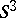 and the framing
and the framing 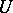 . The Arf-invariant of the function
. The Arf-invariant of the function 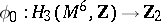 so obtained satisfies the formula
so obtained satisfies the formula 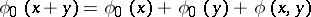
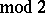 , where
, where 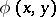 is the intersection form of the
is the intersection form of the  -dimensional homology space on the manifold
-dimensional homology space on the manifold 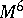 , and is called the Kervaire–Milnor invariant of this manifold with framing
, and is called the Kervaire–Milnor invariant of this manifold with framing 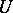 . The pair
. The pair  has a framed surgery to the pair
has a framed surgery to the pair 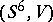 if and only if the Kervaire–Milnor invariant of
if and only if the Kervaire–Milnor invariant of  is zero.
is zero.
Similar constructions have been carried out for  . The Kervaire–Milnor invariant in dimension six is the only invariant of the stable
. The Kervaire–Milnor invariant in dimension six is the only invariant of the stable 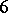 -dimensional framed cobordism and defines an isomorphism
-dimensional framed cobordism and defines an isomorphism 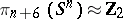 ,
, 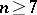 . However, in dimension fourteen it is not a unique invariant of the stable
. However, in dimension fourteen it is not a unique invariant of the stable 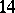 -dimensional framed cobordism, i.e. the stable group
-dimensional framed cobordism, i.e. the stable group 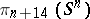 ,
, 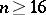 , is defined by framings on the sphere
, is defined by framings on the sphere 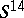 and on
and on 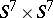 .
.
For references see Kervaire invariant.
Kervaire-Milnor invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kervaire-Milnor_invariant&oldid=17858