Likelihood-ratio test
A statistical test based on the ratio of the greatest values of the likelihood functions under the hypothesis being tested and under all possible states of nature. Let a random variable  have values in the sample space
have values in the sample space 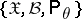 ,
, 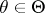 , let the family of measures
, let the family of measures  be absolutely continuous with respect to a
be absolutely continuous with respect to a 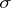 -finite measure
-finite measure 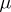 and let
and let 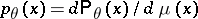 . Suppose it is necessary, via a realization of the random variable
. Suppose it is necessary, via a realization of the random variable  , to test the composite hypothesis
, to test the composite hypothesis 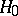 according to which the unknown true value
according to which the unknown true value  of the parameter
of the parameter 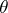 belongs to the set
belongs to the set 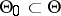 , against the composite alternative
, against the composite alternative 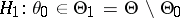 . According to the likelihood-ratio test with significance level
. According to the likelihood-ratio test with significance level 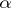 ,
,  , the hypothesis
, the hypothesis 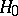 has to be rejected if as a result of the experiment it turns out that
has to be rejected if as a result of the experiment it turns out that 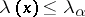 , where
, where 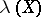 is the statistic of the likelihood-ratio test, defined by:
is the statistic of the likelihood-ratio test, defined by:
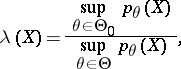 |
while 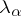 is the critical level determined by the condition that the size of the test,
is the critical level determined by the condition that the size of the test,
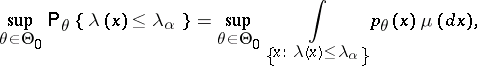 |
is equal to  . In particular, if the set
. In particular, if the set  contains only two points
contains only two points 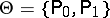 , with densities
, with densities 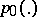 and
and  respectively, corresponding to the concurrent hypotheses which, in this case, are simple, then the statistic of the likelihood-ratio test is simply
respectively, corresponding to the concurrent hypotheses which, in this case, are simple, then the statistic of the likelihood-ratio test is simply
 |
According to the likelihood-ratio test with significance level 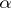 , the hypothesis
, the hypothesis 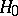 has to be rejected if
has to be rejected if 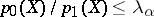 , where the number
, where the number 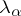 ,
, 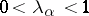 , is determined by the condition
, is determined by the condition
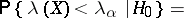 |
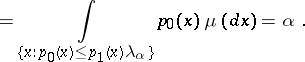 |
The (generalized) likelihood-ratio test was proposed by J. Neyman and E.S. Pearson in 1928. They also proved (1933) that of all level- tests for testing one simple hypothesis against another, the likelihood-ratio test is the most powerful (see Neyman–Pearson lemma).
tests for testing one simple hypothesis against another, the likelihood-ratio test is the most powerful (see Neyman–Pearson lemma).
References
| [1] | J. Neyman, E.S. Pearson, "Joint statistical papers" , Cambridge Univ. Press (1967) |
| [2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
Comments
This test is also called the generalized likelihood-ratio test, or the Wald test.
Likelihood-ratio test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Likelihood-ratio_test&oldid=17836