Rational representation

of an algebraic group 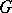over an algebraically closed field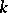

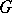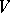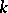A linear representation of on a finite-dimensional vector space over which is a rational homomorphism of 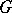into 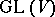. One also says that 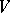is a rational 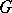-module. Direct sums and tensor products of a finite number of rational representations of 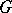are rational representations. Subrepresentations and quotient representations of any rational representation are rational representations. Symmetric and exterior powers of any rational representation are rational representations. The representation contragredient to a rational representation is a rational representation.

If 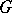is finite, then each of its linear representations will be a rational representation, and the theory of rational representations coincides with the theory of representations of finite groups (cf. Representation of a group). To a large extent, specific methods of the theory of linear algebraic groups are used to study rational representations in case the group under consideration is connected, and the most thoroughly developed theory is that of rational representations of connected semi-simple algebraic groups. Let 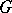be such a group, 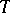a maximal torus, 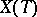its group of rational characters (written additively), 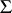the root system of 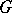with respect to 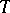, 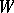its Weyl group, and 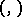a 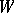-invariant positive-definite non-degenerate scalar product on 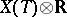. Now let 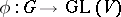be a rational representation. The restriction of 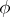to 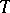decomposes into a direct sum of one-dimensional representations; more precisely,

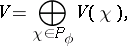where 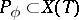is some set of characters of 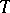, called the weights of the representation, and

The set of weights 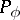is invariant under the action of .

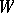If 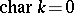, then every rational representation of 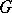is completely reducible, but if 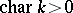, then this is not so (see Mumford hypothesis). Whatever the characteristic of 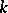, however, there is a complete description of the irreducible rational representations.

Let 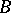be a Borel subgroup in 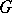containing 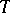and let 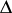be the set of simple roots in 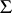defined by 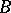. Identify the group 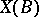of rational characters of 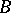with 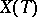. In the space 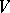, for any irreducible rational representation 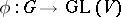there is a unique one-dimensional weight subspace 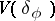, , 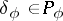invariant under 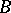. The character 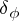is called the highest weight of the irreducible rational representation 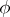; it is dominant, i.e. for any 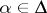, and every other weight 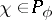has the form

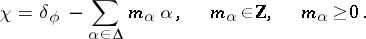The mapping 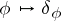defines a bijection between the classes of equivalent irreducible rational representations and the dominant elements of 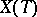. An explicit construction of all irreducible rational representations can be obtained in the following way. Let 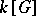be the algebra of regular functions on 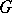. Given any 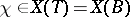, consider the subspace

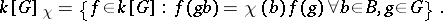It is finite-dimensional and is a rational 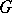-module under the action of 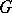by left translation. The geometric meaning of this space is as follows: it can be canonically identified with the set of regular sections of the one-dimensional homogeneous vector bundle over 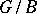determined by the character 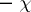. Let 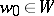be the element mapping positive roots into negative ones. If 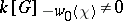, then 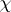is a dominant character and the minimal non-zero 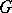-submodule in 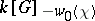is an irreducible rational 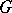-module with highest weight 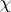. Every irreducible rational 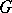-module can be obtained in this way. If 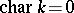, then the 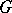-module 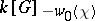is itself irreducible.

To obtain irreducible rational representations, one often applies the above-mentioned operations to given rational representations. For example, if 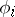is an irreducible rational representation with highest weight 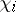, , 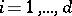then some quotient representation of 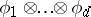is an irreducible rational representation with highest weight 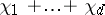(it is called the Cartan product o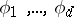f ). If 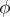is an irreducible rational representation with highest weight 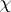, then some quotient representation of 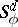is an irreducible rational representation with highest weight 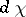. Moreover 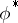is irreducible and its highest weight is .

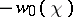Let 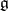be the Lie algebra of 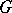(cf. Lie algebra of an algebraic group). If 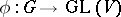is a rational representation, then its differential 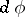is a representation of the Lie algebra 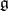. A rational representation 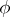is called infinitesimally irreducible if 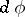is an irreducible representation of the algebra 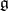. An infinitesimally-irreducible rational representation is irreducible, and when 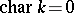, the converse is also true (which largely reduces the theory of rational representations of a group to the theory of representations of its Lie algebra). But when 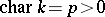, this is not so; the infinitesimally-irreducible rational representations in this case are just those irreducible rational representations with highest weight 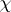for which

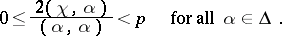Moreover, all the irreducible rational representations can be constructed using the infinitesimally-irreducible ones. More precisely, if 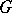is simply connected, that is, if 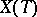coincides with the lattice of weights of the root system 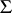, then every irreducible rational representation factors uniquely into a tensor product of the form

where 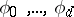are infinitesimally irreducible, and 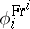is the representation obtained by applying the Frobenius automorphism 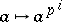(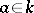, 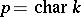) to the matrix entries of the representation .

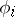References

[1]	A. Borel, "Linear algebraic groups" , Benjamin (1969)
[2]	A. Borel, "Linear representations of semi-simple algebraic groups" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 421–440
[3]	J.E. Humphreys, "Linear algebraic groups" , Springer (1975)
[4]	A. Borel (ed.) R. Carter (ed.) C.W. Curtis (ed.) N. Iwahori (ed.) T.A. Springer (ed.) R. Steinberg (ed.) , Seminar on algebraic groups and related finite groups , Lect. notes in math. , 131 , Springer (1970)
[5]	R.G. Steinberg, "Lectures on Chevalley groups" , Yale Univ. Press (1968)
[6]	R. Steinberg, "Representations of algebraic groups" Nagoya Math. J. , 22 (1963) pp. 33–56
[7]	G. Hochschild, "The structure of Lie groups" , Holden-Day (1965)
[8]	J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972)

Comments

See [a1], especially for complications in .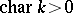

References

[a1]	J.C. Jantzen, "Representations of algebraic groups" , Acad. Press (1987)