Bott-Borel-Weil theorem
A holomorphic action of a complex Lie group 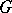 on a holomorphic vector bundle
on a holomorphic vector bundle  is a left holomorphic action,
is a left holomorphic action, 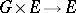 , which projects onto
, which projects onto 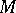 and which sends
and which sends 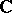 -linearly each vector space fibre
-linearly each vector space fibre 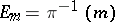 onto
onto 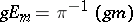 . In this situation
. In this situation 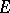 is conveniently said to be
is conveniently said to be 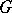 -equivariant. If
-equivariant. If 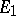 and
and 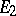 are equivariant bundles over
are equivariant bundles over 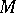 and
and 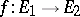 is a mapping of bundles, it is easy to see what is meant by "f is G-equivariant" and also what is meant by "E1 and E2 are equivalent" , as
is a mapping of bundles, it is easy to see what is meant by "f is G-equivariant" and also what is meant by "E1 and E2 are equivalent" , as 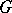 -equivariant vector bundles.
-equivariant vector bundles.
When 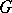 ,
, 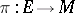 , etc. are as above, one sees that, by restriction, the given action defines a complex linear representation of the stabilizer
, etc. are as above, one sees that, by restriction, the given action defines a complex linear representation of the stabilizer 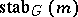 of a point
of a point 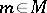 on the
on the 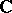 -vectorial fibre
-vectorial fibre 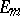 . The equivalence class of this representation depends only on the
. The equivalence class of this representation depends only on the 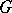 -equivariant holomorphism class of
-equivariant holomorphism class of 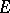 . If
. If 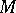 is a homogeneous
is a homogeneous 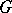 -space, this correspondence between equivalence classes is bijective. This may be explained as follows: If
-space, this correspondence between equivalence classes is bijective. This may be explained as follows: If 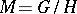 is a complex homogeneous space and
is a complex homogeneous space and  is a holomorphic complex linear representation, one considers the following equivalence relation on
is a holomorphic complex linear representation, one considers the following equivalence relation on 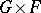 :
:
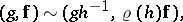 |
where 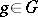 ,
, 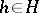 ,
, 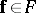 . The quotient space
. The quotient space 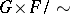 will be denoted by
will be denoted by 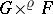 , and the equivalence class of
, and the equivalence class of 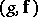 will be denoted by
will be denoted by 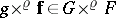 . The formula
. The formula 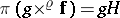 makes
makes 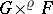 into a vector bundle of fibre type
into a vector bundle of fibre type 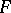 via
via 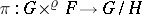 . This fibration is naturally holomorphically
. This fibration is naturally holomorphically 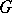 -equivariant via the action
-equivariant via the action 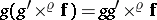 and one checks that the stabilizer,
and one checks that the stabilizer, 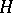 , of the "neutral element" of
, of the "neutral element" of 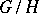 acts (see above) on the "neutral fibre" exactly by the representation
acts (see above) on the "neutral fibre" exactly by the representation 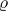 .
.
Below, the case 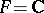 will be regarded in some detail. Thus, the representation
will be regarded in some detail. Thus, the representation 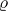 may be interpreted as a multiplicative character
may be interpreted as a multiplicative character 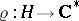 and
and 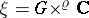 will be a complex line bundle.
will be a complex line bundle.
Background.
Let 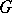 be a semi-simple complex Lie group with Lie algebra
be a semi-simple complex Lie group with Lie algebra 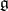 (cf. also Lie group, semi-simple; Lie algebra),
(cf. also Lie group, semi-simple; Lie algebra), 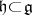 a Cartan subalgebra of
a Cartan subalgebra of 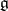 ,
, 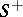 a system of positive roots (cf. Root system),
a system of positive roots (cf. Root system), 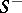 the corresponding system of opposite roots (termed negative), and
the corresponding system of opposite roots (termed negative), and 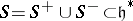 the set of all roots. Let
the set of all roots. Let 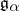 be the root space associated to
be the root space associated to 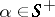 . Then
. Then 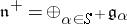 is a nilpotent Lie subalgebra and one defines the maximal solvable subalgebra (the Borel subalgebra)
is a nilpotent Lie subalgebra and one defines the maximal solvable subalgebra (the Borel subalgebra) 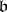 by
by 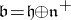 . This is the Lie algebra of a closed complex Lie subgroup
. This is the Lie algebra of a closed complex Lie subgroup 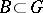 such that
such that 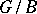 is compact. Finally,
is compact. Finally, 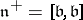 .
.
Note that there is a subspace 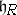 of
of 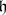 that is, in the vector spaces sense, a real form (that is,
that is, in the vector spaces sense, a real form (that is, 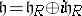 and
and 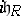 is the Lie subalgebra of a compact connected group). It follows that the restriction to
is the Lie subalgebra of a compact connected group). It follows that the restriction to 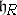 of the Killing form of the complex algebra, denoted by
of the Killing form of the complex algebra, denoted by 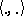 , is a real scalar product. From this one deduces an isomorphism
, is a real scalar product. From this one deduces an isomorphism  and thus a scalar product
and thus a scalar product 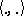 on
on 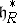 . Notice that the evaluation of the weights of representations (and also of the roots) on
. Notice that the evaluation of the weights of representations (and also of the roots) on 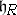 are real numbers. Recall that the closed Weyl chamber
are real numbers. Recall that the closed Weyl chamber 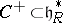 is the set of
is the set of 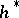 for which
for which 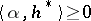 for all
for all 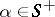 . The Weyl group acts on
. The Weyl group acts on 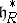 , with
, with 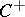 as "fundamental domain" . It is worth noting that while the transformation
as "fundamental domain" . It is worth noting that while the transformation  is not necessarily in the Weyl group, the opposite
is not necessarily in the Weyl group, the opposite  is the transformation
is the transformation 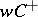 of
of 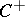 by an element of the Weyl group (in fact, by the longest element). Now consider an irreducible representation
by an element of the Weyl group (in fact, by the longest element). Now consider an irreducible representation 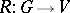 . The theory of H. Weyl classically characterizes such a representation by its dominant weight (cf. also Representation of a Lie algebra). Contrary to tradition, it is perhaps wiser to characterize a representation by its dominated weight. This is the unique weight
. The theory of H. Weyl classically characterizes such a representation by its dominant weight (cf. also Representation of a Lie algebra). Contrary to tradition, it is perhaps wiser to characterize a representation by its dominated weight. This is the unique weight 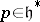 of the representation
of the representation 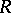 such that the other weights of
such that the other weights of 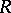 may be obtained from
may be obtained from 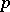 by the addition of an
by the addition of an 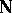 -linear combination of positive roots. In general, the dominated weight of a representation
-linear combination of positive roots. In general, the dominated weight of a representation 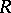 is not the opposite of the dominant weight of
is not the opposite of the dominant weight of 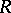 , but the opposite of the dominant weight of the contragredient representation
, but the opposite of the dominant weight of the contragredient representation 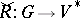 . This dominated weight is always in the opposite of the Weyl chamber.
. This dominated weight is always in the opposite of the Weyl chamber.
Bott–Borel–Weil theorem.
In the above context, consider the hyperplane 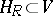 that is the sum of all the proper spaces associated to the weights different from the dominated weight
that is the sum of all the proper spaces associated to the weights different from the dominated weight 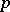 of the representation
of the representation 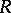 . By the definition of dominated weight, one sees that
. By the definition of dominated weight, one sees that 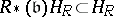 . Now consider the holomorphically trivial bundle
. Now consider the holomorphically trivial bundle 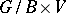 , and make it equivariant by the action
, and make it equivariant by the action 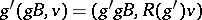 . This
. This 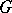 -equivariant bundle is exactly
-equivariant bundle is exactly  , which leads to the equivariant exact sequence of holomorphic bundles:
, which leads to the equivariant exact sequence of holomorphic bundles:
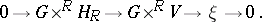 |
In fact, the weight 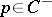 extends to a character
extends to a character 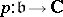 , which can be integrated to give a character
, which can be integrated to give a character 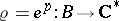 . One easily sees that
. One easily sees that 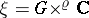 and that the natural action of
and that the natural action of 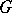 on
on 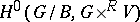 is exactly the representation
is exactly the representation 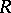 .
.
In this context, the Borel–Weil theorem states:
a) The arrow 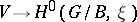 is a
is a 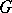 -equivariant isomorphism;
-equivariant isomorphism;
b) 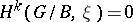 for
for 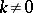 . These results are not unexpected (in case b), at least for those who are familiar with the idea of a sufficiently ample line bundle). This is not at all the case for the generalization to representations of
. These results are not unexpected (in case b), at least for those who are familiar with the idea of a sufficiently ample line bundle). This is not at all the case for the generalization to representations of 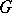 in
in 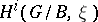 when the line bundle is given by a representation
when the line bundle is given by a representation 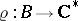 such that the restriction to
such that the restriction to 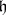 of its derivative
of its derivative  is not the dominated weight of a holomorphic representation of
is not the dominated weight of a holomorphic representation of 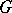 . Indeed, this generalization is the very unexpected Bott–Borel–Weil theorem: Let
. Indeed, this generalization is the very unexpected Bott–Borel–Weil theorem: Let  ,
, 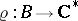 and
and 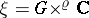 be as above, and let also
be as above, and let also 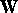 be the Weyl group relative to the Cartan algebra
be the Weyl group relative to the Cartan algebra 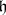 and
and 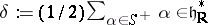 . Then:
. Then:
i) If, for all 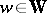 , the quantity
, the quantity 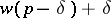 is never the dominated weight of a representation, then all the cohomology groups
is never the dominated weight of a representation, then all the cohomology groups 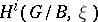 are zero.
are zero.
ii) If there exists an element 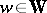 , hence unique with this property, such that
, hence unique with this property, such that 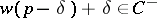 is the dominated weight of a representation
is the dominated weight of a representation 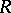 , then:
, then:
A) For 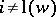 (the length of
(the length of 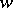 ), the cohomology group
), the cohomology group 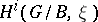 is zero.
is zero.
B) For 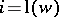 , the natural representation of
, the natural representation of 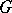 on the cohomology group
on the cohomology group 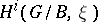 is exactly the representation
is exactly the representation 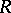 .
.
The proof is essentially a very beautiful application of the relative cohomology of Lie algebras, initiated by C. Chevalley and S. Eilenberg.
References
| [a1] | R. Bott, "Homogeneous vector bundles" Ann. of Math. , 66 (1957) pp. 203–248 |
| [a2] | N.R. Wallach, "Harmonic analysis on homogeneous spaces" , M. Dekker (1973) |
| [a3] | M. Demazure, "A very simple proof of Bott's theorem" Invent. Math. , 33 (1976) |
Bott-Borel-Weil theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bott-Borel-Weil_theorem&oldid=17818