Translativity of a summation method
The property of the method consisting in the preservation of summability of a series after adding to or deleting from it a finite number of terms. More precisely, a summation method  is said to be translative if the summability of the series
is said to be translative if the summability of the series
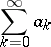 |
to the sum  implies that the series
implies that the series
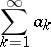 |
is summable by the same method to the sum  , and conversely. For a summation method
, and conversely. For a summation method  defined by transformation of the sequence
defined by transformation of the sequence  into a sequence or function, the property of translativity consists of the equivalence of the conditions
into a sequence or function, the property of translativity consists of the equivalence of the conditions
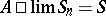 |
and
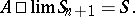 |
If the summation method is defined by a regular matrix 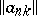 (cf. Regular summation methods), then this means that
(cf. Regular summation methods), then this means that
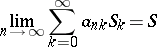 | (1) |
always implies that
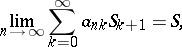 | (2) |
and conversely. In cases when such an inference only holds in one direction, the method is called right translative if (1) implies (2) but the converse is false, or left translative if (2) implies (1) but the converse is false.
Many widely used summation methods have the property of translativity; for example, the Cesàro summation methods  for
for  , the Riesz summation method
, the Riesz summation method 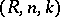 for
for 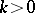 and the Abel summation method are translative; the Borel summation method is left translative.
and the Abel summation method are translative; the Borel summation method is left translative.
References
| [1] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [2] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
Translativity of a summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Translativity_of_a_summation_method&oldid=17808