Diagonalizable algebraic group
An affine algebraic group 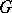 that is isomorphic to a closed subgroup of an algebraic torus. Thus,
that is isomorphic to a closed subgroup of an algebraic torus. Thus, 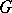 is isomorphic to a closed subgroup of a multiplicative group of all diagonal matrices of given size. If
is isomorphic to a closed subgroup of a multiplicative group of all diagonal matrices of given size. If 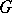 is defined over a field
is defined over a field 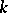 and the isomorphism is defined over
and the isomorphism is defined over 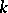 , the diagonalizable algebraic group
, the diagonalizable algebraic group  is said to be split (or decomposable) over
is said to be split (or decomposable) over 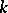 .
.
Any closed subgroup 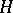 in a diagonalizable algebraic group
in a diagonalizable algebraic group 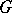 , as well as the image of
, as well as the image of 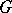 under an arbitrary rational homomorphism
under an arbitrary rational homomorphism 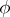 , is a diagonalizable algebraic group. If, in addition,
, is a diagonalizable algebraic group. If, in addition, 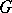 is defined and split over a field
is defined and split over a field  , while
, while 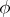 is defined over
is defined over 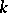 , then both
, then both 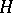 and
and 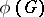 are defined and split over
are defined and split over 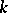 .
.
A diagonalizable algebraic group is split over 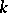 if and only if elements in the group
if and only if elements in the group 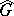 of its rational characters are rational over
of its rational characters are rational over 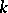 . If
. If 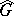 contains no non-unit elements rational over
contains no non-unit elements rational over 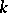 , the diagonalizable algebraic group
, the diagonalizable algebraic group 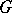 is said to be anisotropic over
is said to be anisotropic over 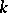 . Any diagonalizable algebraic group
. Any diagonalizable algebraic group 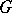 defined over the field
defined over the field 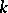 is split over some finite separable extension of
is split over some finite separable extension of 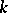 .
.
A diagonalizable algebraic group is connected if and only if it is an algebraic torus. The connectedness of 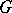 is also equivalent to the absence of torsion in
is also equivalent to the absence of torsion in 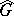 . For any diagonalizable algebraic group
. For any diagonalizable algebraic group  defined over
defined over  , the group
, the group 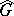 is a finitely-generated Abelian group without
is a finitely-generated Abelian group without 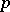 -torsion, where
-torsion, where 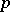 is the characteristic of
is the characteristic of  .
.
Any diagonalizable algebraic group 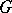 which is defined and split over a field
which is defined and split over a field 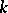 is the direct product of a finite Abelian group and an algebraic torus defined and split over
is the direct product of a finite Abelian group and an algebraic torus defined and split over 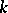 . Any diagonalizable algebraic group
. Any diagonalizable algebraic group 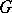 which is connected and defined over a field
which is connected and defined over a field 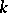 contains a largest anisotropic subtorus
contains a largest anisotropic subtorus 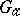 and a largest subtorus
and a largest subtorus 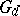 which is split over
which is split over 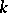 ; for these,
; for these, 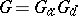 , and
, and 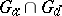 is a finite set.
is a finite set.
If a diagonalizable algebraic group 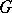 is defined over a field
is defined over a field 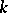 and
and  is the Galois group of the separable closure of
is the Galois group of the separable closure of  , then
, then 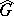 is endowed with a continuous action of
is endowed with a continuous action of  . If, in addition,
. If, in addition,  is a rational homomorphism between diagonalizable algebraic groups, while
is a rational homomorphism between diagonalizable algebraic groups, while 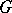 ,
, 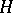 and
and 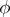 are defined over
are defined over 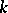 , then the homomorphism
, then the homomorphism 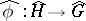 is
is 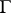 -equivariant (i.e. is a homomorphism of
-equivariant (i.e. is a homomorphism of 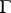 -modules). The resulting contravariant functor from the category of diagonalizable
-modules). The resulting contravariant functor from the category of diagonalizable 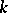 -groups and their
-groups and their 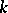 -morphisms into the category of finitely-generated Abelian groups without
-morphisms into the category of finitely-generated Abelian groups without 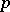 -torsion with a continuous action of the group
-torsion with a continuous action of the group 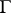 and their
and their 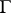 -equivariant homomorphisms is an equivalence of these categories.
-equivariant homomorphisms is an equivalence of these categories.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | T. Ono, "Arithmetic of algebraic tori" Ann. of Math. , 74 : 1 (1961) pp. 101–139 |
Comments
References
| [a1] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
Diagonalizable algebraic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagonalizable_algebraic_group&oldid=17794