Integral curve
The graph of a solution  of a normal system
of a normal system
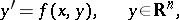 |
of ordinary differential equations. For example, the integral curves of the equation
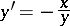 |
are the circles 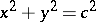 , where
, where  is an arbitrary constant. The integral curve is often identified with the solution. The geometric meaning of the integral curves of a scalar equation
is an arbitrary constant. The integral curve is often identified with the solution. The geometric meaning of the integral curves of a scalar equation
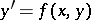 | (*) |
is the following. The equation (*) defines a direction field on the plane, that is, a field of direction vectors such that at each point  the tangent of the angle of inclination of the vector with the
the tangent of the angle of inclination of the vector with the  -axis is equal to
-axis is equal to  . The integral curves of (*) are then the curves that at each point have a tangent coinciding with the vector of the direction field at this point. The integral curves of (*) fill out the entire region in which the function
. The integral curves of (*) are then the curves that at each point have a tangent coinciding with the vector of the direction field at this point. The integral curves of (*) fill out the entire region in which the function 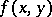 satisfies conditions ensuring the existence and uniqueness of the Cauchy problem; the curves nowhere intersect one another and are nowhere tangent to one another.
satisfies conditions ensuring the existence and uniqueness of the Cauchy problem; the curves nowhere intersect one another and are nowhere tangent to one another.
References
| [1] | I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian) |
Comments
A normal system of differential equations is a system of differential equations of the form
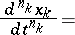 |
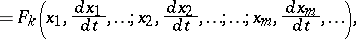 |
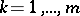 , such that the function
, such that the function 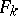 only depends on the
only depends on the 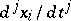 for
for 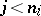 ,
, 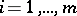 .
.
References
| [a1] | G. Birkhoff, G.-C. Rota, "Ordinary differential equations" , Ginn (1962) pp. Chapt. V §5 |
| [a2] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) pp. §§3.6, 3.51, 4.7, A.5 |
Integral curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_curve&oldid=17766