Particular solutions of the Airy equation.
The first Airy function (or simply the Airy function) is defined by
For complex values of 
where 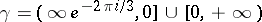 is a contour in the complex
is a contour in the complex 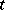 -plane. The second Airy function is defined by
-plane. The second Airy function is defined by
The functions 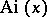 and
and 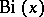 are real for real
are real for real  .
.
A second collection of Airy functions was introduced by V.A. Fock [V.A. Fok]:
in this case 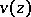 is called the Airy–Fok function (Airy–Fock function). The following identities hold:
is called the Airy–Fok function (Airy–Fock function). The following identities hold:
 | (1) |
Any two of 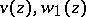 and
and 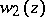 are linearly independent.
are linearly independent.
The most important Airy function is 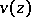 (or
(or 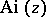 ). Its asymptotic behaviour on the real axis is given by
). Its asymptotic behaviour on the real axis is given by
so 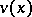 decreases rapidly for
decreases rapidly for 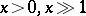 and oscillates strongly for
and oscillates strongly for 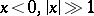 . The functions
. The functions  and
and 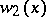 increase exponentially as
increase exponentially as 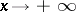 . For complex
. For complex  the Airy functions have the following asymptotic expansions as
the Airy functions have the following asymptotic expansions as 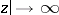 :
:
 | (2) |
where
The asymptotic expansion of 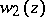 is of the form (2), but it is valid in the sector
is of the form (2), but it is valid in the sector
Here 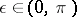 is arbitrary, the branches of
is arbitrary, the branches of  and
and 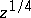 are positive on the semi-axis
are positive on the semi-axis 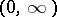 , and the asymptotic expansions are uniform with respect to
, and the asymptotic expansions are uniform with respect to 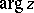 and can be differentiated term by term any number of times. In the remaining sector
and can be differentiated term by term any number of times. In the remaining sector 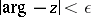 the asymptotic expansion of
the asymptotic expansion of 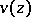 is expressed in terms of those of
is expressed in terms of those of 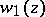 and
and 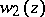 by means of (1); hence, the asymptotic expansion of
by means of (1); hence, the asymptotic expansion of 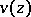 has a different form in different sectors of the complex
has a different form in different sectors of the complex  -plane. This fact was first established by G.G. Stokes [2] and is called the Stokes phenomenon.
-plane. This fact was first established by G.G. Stokes [2] and is called the Stokes phenomenon.
The Airy functions occur in the study of integrals of rapidly-oscillating functions, of the form
for 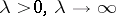 . Here
. Here 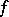 and
and  are smooth functions,
are smooth functions, 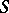 is real and
is real and 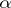 is a real parameter. If for small values of
is a real parameter. If for small values of 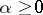 the phase
the phase 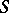 has two close non-degenerate stationary points
has two close non-degenerate stationary points 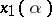 and
and 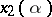 that coincide for
that coincide for 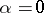 , for example, if
, for example, if
then for small values of 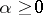 , as
, as 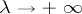 , the contribution to the asymptotics of the integral coming from a neighbourhood of the point
, the contribution to the asymptotics of the integral coming from a neighbourhood of the point 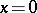 can be expressed in terms of the Airy function
can be expressed in terms of the Airy function  and its derivative (see [6]). Integrals of this kind occur in the study of short-wave fields near a simple focus (see [7] and [8]); the Airy functions arose in connection with the study of this problem [1].
and its derivative (see [6]). Integrals of this kind occur in the study of short-wave fields near a simple focus (see [7] and [8]); the Airy functions arose in connection with the study of this problem [1].
Consider the second-order differential equation
 | (3) |
where 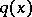 is a smooth real-valued function on the interval
is a smooth real-valued function on the interval 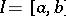 and
and 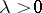 is a large parameter. The zeros of
is a large parameter. The zeros of 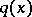 are called turning points (or transfer points) of the equation (3). Let
are called turning points (or transfer points) of the equation (3). Let
(such a point is called simple),
Set
Equation (3) has linearly independent solutions 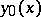 and
and 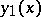 such that, as
such that, as 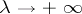 ,
,
uniformly with respect to  .
.
This result has been generalized in various directions: asymptotic series have been obtained for the solutions, the case 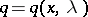 has been studied (for example, if
has been studied (for example, if 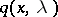 can be expanded in an asymptotic series
can be expanded in an asymptotic series 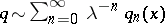 as
as 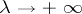 ), and the asymptotic behaviour of the solutions near multiple turning points has been investigated. Other generalizations concern the equation
), and the asymptotic behaviour of the solutions near multiple turning points has been investigated. Other generalizations concern the equation
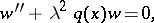 | (4) |
where the function 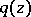 is analytic in a domain
is analytic in a domain 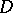 of the complex
of the complex  -plane. Let
-plane. Let 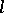 be the maximal connected component of the level line
be the maximal connected component of the level line
emanating from a turning point 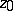 and containing no other turning points; then
and containing no other turning points; then 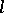 is called a Stokes line. If
is called a Stokes line. If 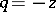 (that is, (4) is the Airy equation), then the Stokes lines are the rays
(that is, (4) is the Airy equation), then the Stokes lines are the rays 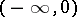 and
and 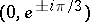 . Analogously, if
. Analogously, if 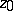 is a simple turning point of (4), then there are three Stokes lines
is a simple turning point of (4), then there are three Stokes lines 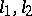 and
and 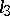 emanating from it and the angle between adjacent lines at
emanating from it and the angle between adjacent lines at 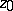 is equal to
is equal to 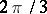 . Let
. Let 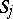 be a neighbourhood of
be a neighbourhood of 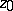 from which a neighbourhood of the Stokes line
from which a neighbourhood of the Stokes line  ,
, 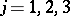 , has been removed. For a suitable numbering of the
, has been removed. For a suitable numbering of the 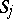 , equation (4) has three solutions
, equation (4) has three solutions 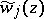 ,
,  , such that, as
, such that, as 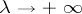 ,
,
for 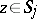 .
.
The Airy functions also occur in the study of asymptotic solutions of ordinary differential equations and systems of higher order near simple turning points.
References
| [1] | G.B. Airy, Trans. Cambridge Philos. Soc. , 6 (1838) pp. 379–402 |
| [2] | G.G. Stokes, Trans. Cambridge Philos. Soc. , 10 (1857) pp. 105–128 |
| [3] | V.A. Fok, "Tables of the Airy functions" , Moscow (1946) (In Russian) |
| [4] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [5] | V.M. Babich, V.S. Buldyrev, "Asymptotic methods in the diffraction of short waves" , Moscow (1972) (In Russian) (Translation forthcoming: Springer) |
| [6] | M.V. Fedoryuk, "The saddle-point method" , Moscow (1977) (In Russian) |
| [7] | E.M. Lifshits, "The classical theory of fields" , Addison-Wesley (1951) (Translated from Russian) |
| [8] | V.P. Maslov, M.V. Fedoryuk, "Quasi-classical approximation for the equations of quantum mechanics" , Reidel (1981) (Translated from Russian) |
| [9] | A.A. Dorodnitsyn, "Asymptotic laws of distribution of the characteristic values for certain types of second-order differential equations" Uspekhi Mat. Nauk , 6 : 7 (1952) pp. 3–96 (In Russian) |
| [10] | W. Wasov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965) |
| [11] | M.V. Fedoryuk, "Asymptotic methods for linear ordinary differential equations" , Moscow (1983) (In Russian) |
The Airy function can be expressed in terms of modified Bessel functions of the third kind:
The function  satisfies the differential equation
satisfies the differential equation 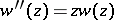 , cf. [a2].
, cf. [a2].
References
| [a1] | F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974) |
| [a2] | N.N. Lebedev, "Special functions and their applications" , Dover, reprint (1972) (Translated from Russian) |
How to Cite This Entry:
Airy functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Airy_functions&oldid=17747
This article was adapted from an original article by M.V. Fedoryuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article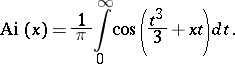

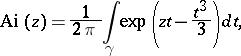
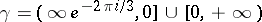 is a contour in the complex
is a contour in the complex 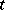 -plane. The second Airy function is defined by
-plane. The second Airy function is defined by
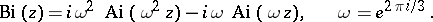
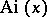 and
and 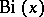 are real for real
are real for real  .
.
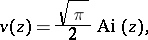
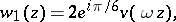

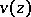 is called the Airy–Fok function (Airy–Fock function). The following identities hold:
is called the Airy–Fok function (Airy–Fock function). The following identities hold:

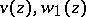 and
and 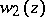 are linearly independent.
are linearly independent.
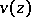 (or
(or 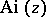 ). Its asymptotic behaviour on the real axis is given by
). Its asymptotic behaviour on the real axis is given by
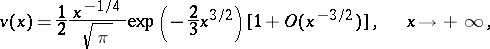
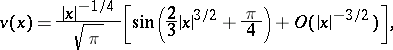

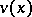 decreases rapidly for
decreases rapidly for 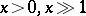 and oscillates strongly for
and oscillates strongly for 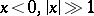 . The functions
. The functions  and
and 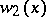 increase exponentially as
increase exponentially as 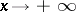 . For complex
. For complex  the Airy functions have the following asymptotic expansions as
the Airy functions have the following asymptotic expansions as 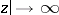 :
:

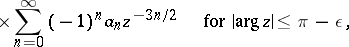
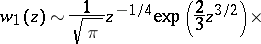

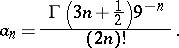
 is of the form (2), but it is valid in the sector
is of the form (2), but it is valid in the sector
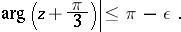
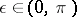 is arbitrary, the branches of
is arbitrary, the branches of  and
and 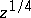 are positive on the semi-axis
are positive on the semi-axis 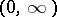 , and the asymptotic expansions are uniform with respect to
, and the asymptotic expansions are uniform with respect to 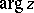 and can be differentiated term by term any number of times. In the remaining sector
and can be differentiated term by term any number of times. In the remaining sector 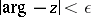 the asymptotic expansion of
the asymptotic expansion of 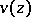 is expressed in terms of those of
is expressed in terms of those of 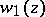 and
and 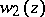 by means of (1); hence, the asymptotic expansion of
by means of (1); hence, the asymptotic expansion of 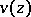 has a different form in different sectors of the complex
has a different form in different sectors of the complex  -plane. This fact was first established by G.G. Stokes [2] and is called the Stokes phenomenon.
-plane. This fact was first established by G.G. Stokes [2] and is called the Stokes phenomenon.
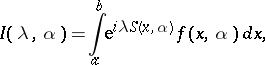
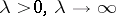 . Here
. Here 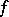 and
and  are smooth functions,
are smooth functions, 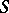 is real and
is real and 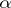 is a real parameter. If for small values of
is a real parameter. If for small values of 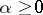 the phase
the phase 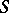 has two close non-degenerate stationary points
has two close non-degenerate stationary points 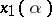 and
and 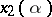 that coincide for
that coincide for 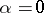 , for example, if
, for example, if
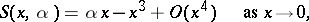
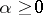 , as
, as 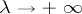 , the contribution to the asymptotics of the integral coming from a neighbourhood of the point
, the contribution to the asymptotics of the integral coming from a neighbourhood of the point 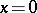 can be expressed in terms of the Airy function
can be expressed in terms of the Airy function  and its derivative (see [6]). Integrals of this kind occur in the study of short-wave fields near a simple focus (see [7] and [8]); the Airy functions arose in connection with the study of this problem [1].
and its derivative (see [6]). Integrals of this kind occur in the study of short-wave fields near a simple focus (see [7] and [8]); the Airy functions arose in connection with the study of this problem [1].

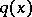 is a smooth real-valued function on the interval
is a smooth real-valued function on the interval 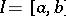 and
and 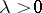 is a large parameter. The zeros of
is a large parameter. The zeros of 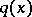 are called turning points (or transfer points) of the equation (3). Let
are called turning points (or transfer points) of the equation (3). Let
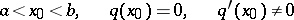
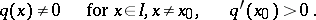

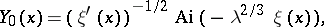

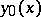 and
and 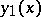 such that, as
such that, as 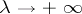 ,
,
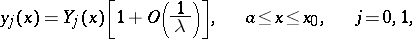
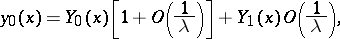

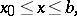
 .
.
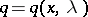 has been studied (for example, if
has been studied (for example, if 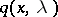 can be expanded in an asymptotic series
can be expanded in an asymptotic series 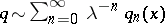 as
as 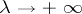 ), and the asymptotic behaviour of the solutions near multiple turning points has been investigated. Other generalizations concern the equation
), and the asymptotic behaviour of the solutions near multiple turning points has been investigated. Other generalizations concern the equation
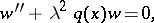
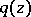 is analytic in a domain
is analytic in a domain 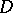 of the complex
of the complex  -plane. Let
-plane. Let 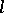 be the maximal connected component of the level line
be the maximal connected component of the level line
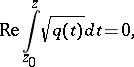
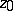 and containing no other turning points; then
and containing no other turning points; then 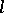 is called a Stokes line. If
is called a Stokes line. If 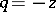 (that is, (4) is the Airy equation), then the Stokes lines are the rays
(that is, (4) is the Airy equation), then the Stokes lines are the rays 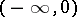 and
and 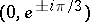 . Analogously, if
. Analogously, if 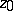 is a simple turning point of (4), then there are three Stokes lines
is a simple turning point of (4), then there are three Stokes lines 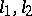 and
and 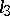 emanating from it and the angle between adjacent lines at
emanating from it and the angle between adjacent lines at 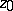 is equal to
is equal to 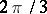 . Let
. Let 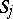 be a neighbourhood of
be a neighbourhood of 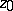 from which a neighbourhood of the Stokes line
from which a neighbourhood of the Stokes line  ,
, 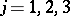 , has been removed. For a suitable numbering of the
, has been removed. For a suitable numbering of the 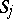 , equation (4) has three solutions
, equation (4) has three solutions 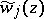 ,
,  , such that, as
, such that, as 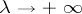 ,
,
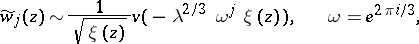
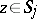 .
.
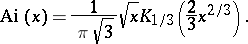
 satisfies the differential equation
satisfies the differential equation 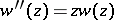 , cf. [a2].
, cf. [a2].