X-ray transform
In 1963, A.M. Cormack introduced a powerful diagnostic tool in radiology, computerized tomography, which is based on the mathematical properties of the X-ray transform in the Euclidean plane [a1] (cf. also Tomography). For a compactly supported continuous function  , its X-ray transform
, its X-ray transform  is a function defined on the family of all straight lines
is a function defined on the family of all straight lines  in
in  as follows: let the unit vector
as follows: let the unit vector  represent the direction of
represent the direction of  and let
and let  be its signed distance to the origin, so that
be its signed distance to the origin, so that  is represented by the pair
is represented by the pair  (as well as
(as well as  ); then
); then
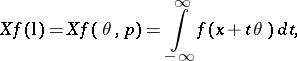 |
where  is an arbitrary point on the line
is an arbitrary point on the line  . This transform had already been considered in 1917 by J. Radon, who found its inverse with the help of its adjoint, given by the average value
. This transform had already been considered in 1917 by J. Radon, who found its inverse with the help of its adjoint, given by the average value  of the
of the 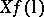 over the family of all lines
over the family of all lines 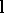 which are at a (signed) distance
which are at a (signed) distance 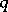 from the point
from the point  , namely,
, namely,
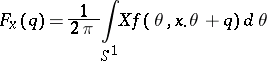 |
where 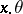 is the Euclidean inner product between
is the Euclidean inner product between  and
and 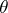 . Radon then showed that the function
. Radon then showed that the function 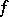 can be recovered by the formula
can be recovered by the formula
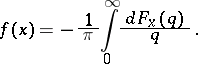 |
The generalization of the X-ray transform to Euclidean spaces of arbitrary dimension and replacing the family of all lines by the family of all affine subspaces of a fixed dimension is known as the Radon transform [a1]. For the Radon transform in the broader context of symmetric spaces, see also [a2].
Note that the adjoint of the X-ray transform can be traced back to the Buffon needle problem (1777): find the average number of times that a needle of length  , dropped at random on a plane, intersects one of the lines of a family of parallel lines located at a distance
, dropped at random on a plane, intersects one of the lines of a family of parallel lines located at a distance 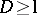 (cf. also Buffon problem). As explained in [a3], Chapt. 5, the solution leads to the consideration of a measure
(cf. also Buffon problem). As explained in [a3], Chapt. 5, the solution leads to the consideration of a measure  on the space of all lines in the plane and of
on the space of all lines in the plane and of  invariance under all rigid motions. This measure induces a functional
invariance under all rigid motions. This measure induces a functional  on the family of compact sets
on the family of compact sets  by
by
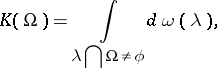 |
which is basically the adjoint of the X-ray transform. Thus, among the generalizations of the X-ray transform and its adjoint, one also finds basic links to integral geometry [a3], [a6], combinatorial geometry [a4], convex geometry [a5], as well as the Pompeiu problem.
References
| [a1] | F. Natterer, "The mathematics of computerized tomography" , Wiley (1986) |
| [a2] | S. Helgason, "Geometric analysis on symmetric spaces" , Amer. Math. Soc. (1994) |
| [a3] | L.A. Santaló, "Integral geometry and geometric probability" , Encycl. Math. Appl. , Addison-Wesley (1976) |
| [a4] | R.V. Ambartzumian, "Combinatorial integral geometry" , Wiley (1982) |
| [a5] | "Handbook of convex geometry" P.M. Gruber (ed.) J.M. Wills (ed.) , 1; 2 , North-Holland (1993) |
| [a6] | C.A. Berenstein, E.L. Grinberg, "A short bibliography on integral geometry" Gaceta Matematica (R. Acad. Sci. Spain) , 1 (1998) pp. 189–194 |
X-ray transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=X-ray_transform&oldid=17712