Ramified prime ideal

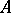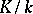A prime ideal in a Dedekind ring which divides the discriminant of a finite separable extension , where is the field of fractions of . Such ideals are the only ideals that are ramified in the extension . A prime ideal of a ring is ramified in if the following product representation holds in the integral closure of 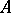in the field :

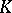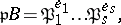where 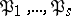are prime ideals in and at least one of the numbers 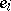is greater than 1. The number is called the ramification index of over .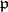

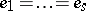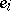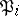If is a Galois extension with Galois group , then and is precisely the order of the inertia subgroup of in :

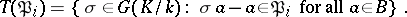Other, more refined, characteristics of the ramification are given by the higher ramification groups 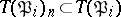, 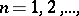defined as follows:

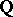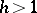Let ; by Minkowski's theorem, for any finite extension of the field of rational numbers there exists a ramified prime ideal. This is not true for arbitrary algebraic number fields: If the field has class number , i.e. has a non-trivial ideal class group, then there exist unramified extensions over , i.e. extensions having no ramified prime ideal. An example of such an extension is the Hilbert class field of the field 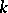; e.g., the field is the Hilbert class field of 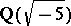and is unramified over .

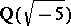References

[1]	Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1987) (Translated from Russian) (German translation: Birkhäuser, 1966)
[2]	J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986)
[3]	S. Lang, "Algebraic number theory" , Addison-Wesley (1970)