Wishart distribution
The joint distribution of the elements from the sample covariance matrix of observations from a multivariate normal distribution. Let the results of observations have a 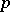 -dimensional normal distribution
-dimensional normal distribution 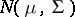 with vector mean
with vector mean 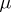 and covariance matrix
and covariance matrix 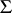 . Then the joint density of the elements of the matrix
. Then the joint density of the elements of the matrix  is given by the formula
is given by the formula
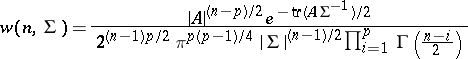 |
(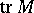 denotes the trace of a matrix
denotes the trace of a matrix 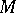 ), if the matrix
), if the matrix 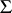 is positive definite, and
is positive definite, and 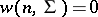 in other cases. The Wishart distribution with
in other cases. The Wishart distribution with  degrees of freedom and with matrix
degrees of freedom and with matrix 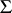 is defined as the
is defined as the 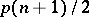 -dimensional distribution
-dimensional distribution 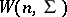 with density
with density 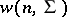 . The sample covariance matrix
. The sample covariance matrix 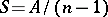 , which is an estimator for the matrix
, which is an estimator for the matrix 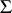 , has a Wishart distribution.
, has a Wishart distribution.
The Wishart distribution is a basic distribution in multivariate statistical analysis; it is the 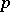 -dimensional generalization (in the sense above) of the
-dimensional generalization (in the sense above) of the 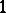 -dimensional "chi-squared" distribution.
-dimensional "chi-squared" distribution.
If the independent random vectors 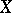 and
and 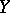 have Wishart distributions
have Wishart distributions 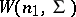 and
and 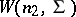 , respectively, then the vector
, respectively, then the vector 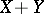 has the Wishart distribution
has the Wishart distribution 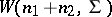 .
.
The Wishart distribution was first used by J. Wishart [1].
References
| [1] | J. Wishart, Biometrika A , 20 (1928) pp. 32–52 |
| [2] | T.W. Anderson, "An introduction to multivariate statistical analysis" , Wiley (1958) |
Comments
References
| [a1] | A.M. Khirsagar, "Multivariate analysis" , M. Dekker (1972) |
| [a2] | R.J. Muirhead, "Aspects of multivariate statistical theory" , Wiley (1982) |
Wishart distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wishart_distribution&oldid=17673