Chebyshev net
From Encyclopedia of Mathematics
A net in which the tangent vectors to each family of lines can be parallel displaced along the lines of the other family. A Chebyshev net of the first kind is a net 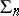 such that, for each
such that, for each 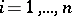 , the directions of the distribution
, the directions of the distribution 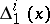 are parallel in the connection
are parallel in the connection  along any integral curve of any of the other distributions
along any integral curve of any of the other distributions 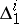 defined by this net. A Chebyshev net of the second kind is a net
defined by this net. A Chebyshev net of the second kind is a net 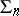 (
(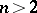 ) such that for each
) such that for each 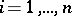 , the subspaces
, the subspaces 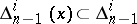 are parallel in the connection
are parallel in the connection  along the integral curves of the distribution
along the integral curves of the distribution 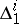 .
.
Introduced by P.L. Chebyshev (1878).
References
| [1] | P.L. Chebyshev, , Collected works , 5 , Moscow-Leningrad (1951) pp. 165–170 (In Russian) |
How to Cite This Entry:
Chebyshev net. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_net&oldid=17668
Chebyshev net. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_net&oldid=17668
This article was adapted from an original article by V.T. Bazylev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article