Appell equations

Ordinary differential equations which describe the motions of both holonomic and non-holonomic systems, established by P.E. Appell [1]. They are sometimes referred to as Gibbs–Appell equations, since they were first proposed by J.W. Gibbs [3] for holonomic systems. The Appell equations in independent Lagrange coordinates 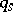(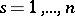) have the form of second-order equations

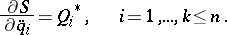(1)

Here

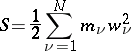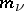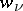( and are the masses and the accelerations of the 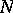points of the system) is the energy of acceleration of the system, which is so expressed that it contains the second derivatives of the coordinates , , 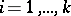only, the variations of which are considered as independent; 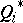are the generalized forces corresponding to the coordinates 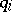, obtained as coefficients in front of the independent variations 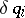in the expression for the work of the given active forces 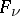corresponding to virtual displacements :

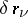In evaluating 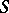and 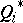the dependent variables 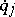(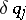) 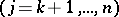are expressed in terms of the independent velocities (variations) by solving the 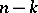non-holonomic constraint equations (cf. Non-holonomic systems), expressed in the generalized coordinates 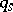(and by solving the equations for 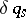obtained from them). Differentiation with respect to the time 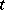of the expressions found for yields expressions for 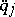in terms of .

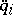Equations (1), together with the 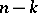equations of the non-integrable constraints, form a system (of order 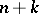) of differential equations involving the unknowns .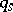

For a holonomic system 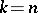, all velocities 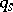and variations 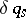are independent, 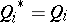, and equations (1) are a different notation for the Lagrange equations (in mechanics)) of the second kind.

Appell's equations in quasi-coordinates 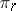, where

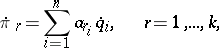(2)

have the form

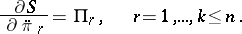(3)

Here 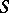is the energy of acceleration, expressed in terms of the second "derivatives" 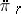(with respect to the time) of the quasi-coordinates, and 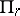are the generalized forces corresponding to the quasi-coordinates. Equations (3), together with the 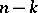equations of the non-integrable constraints and the 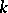equations (2), form a system of 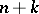differential equations of the first order with the same number of unknowns 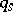, , 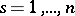and , .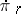

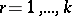Appell's equations are the most general equations of motion of mechanical systems.

References

[1]	P.E. Appell, "Sur une forme génerale des équations de la dynamique" C.R. Acad. Sci. Paris Sér. I Math. , 129 (1899)
[2]	P.E. Appell, "Sur une forme générale des équations de la dynamique et sur le principe de Gauss" J. Reine Angew. Math. , 122 (1900) pp. 205–208
[3]	J.W. Gibbs, "On the fundamental formula of dynamics" Amer. J. Math. , 2 (1879) pp. 49–64

References

[a1]	E.T. Whittaker, "Analytical dynamics" , Cambridge Univ. Press (1927) pp. 258