Affine differential geometry
The branch of geometry dealing with the differential-geometric properties of curves and surfaces that are invariant under transformations of the affine group or its subgroups. The differential geometry of equi-affine space has been most thoroughly studied.
In an equi-affine plane any two vectors 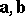 have an invariant
have an invariant 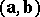 — the surface area of the parallelogram constructed on
— the surface area of the parallelogram constructed on  and
and 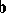 . With the aid of this concept, the invariant parameter
. With the aid of this concept, the invariant parameter
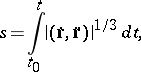 |
known as the equi-affine arc length, can be constructed for a non-rectilinear curve 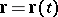 . The differential invariant
. The differential invariant
 |
is called the equi-affine curvature of the plane curve. Constant equi-affine curvature characterizes curves of the second order. A natural equation 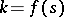 determines a curve up to an equi-affine transformation. The vector
determines a curve up to an equi-affine transformation. The vector 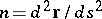 is directed along the affine normal to a plane curve; the affine normal at a point
is directed along the affine normal to a plane curve; the affine normal at a point  ,
, 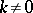 , is the tangent to the locus of the mid-chords of the curve parallel to the tangent at
, is the tangent to the locus of the mid-chords of the curve parallel to the tangent at 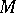 , and coincides with the diameter of the parabola which has third-order contact with the curve at
, and coincides with the diameter of the parabola which has third-order contact with the curve at 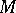 .
.
Passing to the general affine group, two more invariants of the curve are considered: the affine arc length 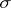 and the affine curvature
and the affine curvature 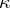 . They can be expressed in terms of the invariants
. They can be expressed in terms of the invariants  and
and 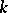 introduced above:
introduced above:
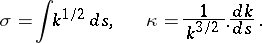 |
(In equi-affine geometry, the magnitudes  and
and 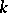 themselves are called the affine arc length and the affine curvature, for the sake of brevity.) The centro-affine arc length, centro-affine curvature, equi-centro-affine arc length and equi-centro-affine curvature of a plane curve are constructed in a similar manner.
themselves are called the affine arc length and the affine curvature, for the sake of brevity.) The centro-affine arc length, centro-affine curvature, equi-centro-affine arc length and equi-centro-affine curvature of a plane curve are constructed in a similar manner.
In equi-affine space it is possible to assign to any three vectors 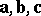 the invariant
the invariant 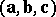 , which is the volume of the oriented parallelepiped defined by these vectors. The natural parameter (equi-affine arc length) of a curve
, which is the volume of the oriented parallelepiped defined by these vectors. The natural parameter (equi-affine arc length) of a curve 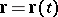 (
(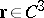 ) is defined by the formula
) is defined by the formula
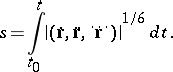 |
The differential invariants 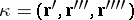 ,
, 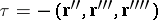 , where the primes denote differentiation with respect to the natural parameter, are called, respectively, the equi-affine curvature and the equi-affine torsion of the spatial curve. The study of the curve is reduced to selecting some moving frame; the frame formed by the vectors
, where the primes denote differentiation with respect to the natural parameter, are called, respectively, the equi-affine curvature and the equi-affine torsion of the spatial curve. The study of the curve is reduced to selecting some moving frame; the frame formed by the vectors
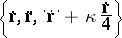 |
and defined by the fourth-order differential neighbourhood of the curve being studied, is especially important. The centro-affine theory of spatial curves has been developed [5].
The following tensor is constructed for a non-developable surface 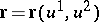 in equi-affine space:
in equi-affine space:
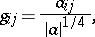 |
where 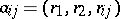 ,
, 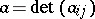 ,
, 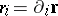 ,
, 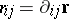 . The vector
. The vector
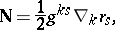 |
where 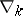 is the symbol of the covariant derivative with respect to the metric tensor
is the symbol of the covariant derivative with respect to the metric tensor 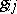 , determines the direction of the affine normal to the surface. The affine normal passes through the centre of the osculating Lie quadric. The derivational equations
, determines the direction of the affine normal to the surface. The affine normal passes through the centre of the osculating Lie quadric. The derivational equations
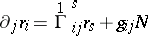 |
define an intrinsic connection of the first kind 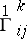 of the surface. There also arises at the same time an intrinsic connection of the second kind
of the surface. There also arises at the same time an intrinsic connection of the second kind 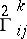 , defined by the derivational equations
, defined by the derivational equations
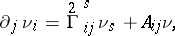 |
where  is a covariant vector defining the tangent plane to the surface and subject to the normalization condition
is a covariant vector defining the tangent plane to the surface and subject to the normalization condition 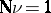 . The connections
. The connections
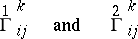 |
are conjugate with respect to the tensor 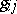 in the sense of A.P. Norden [3]. The tensor
in the sense of A.P. Norden [3]. The tensor
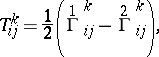 |
which also plays a major part in projective differential geometry, makes it possible to construct the symmetric covariant tensor
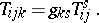 |
The two principal surface forms are also constructed: the quadratic form
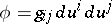 |
and the Fubini–Pick cubic form
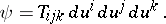 |
These forms are connected by the apolarity condition
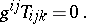 |
Two such forms, which satisfy supplementary differential conditions, determine the surface up to equi-affine transformations. All these statements have appropriate generalizations in the multi-dimensional case.
Many specific classes of surfaces are distinguished in affine and equi-affine spaces: affine spheres (for which the affine normals form a bundle), affine surfaces of revolution (the affine normals intersect one proper or improper straight line), affine minimal surfaces, etc.
In addition to curves and surfaces, other geometrical objects in equi-affine space are also studied, such as congruences and complexes of straight lines, vector fields, etc.
In parallel with equi-affine differential geometry, development is also in progress of the differential geometry of the general affine group and of its other subgroups both in three-dimensional and in multi-dimensional spaces (centro-affine, equi-centro-affine, affine-symplectic, bi-affine, etc.).
References
| [1] | W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Affine Differentialgeometrie" , 2 , Springer (1923) |
| [2] | E. Salkowski, "Affine Differentialgeometrie" , de Gruyter (1934) |
| [3] | A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian) |
| [4] | G.F. Laptev, "Differential geometry of multi-dimensional surfaces" Itogi Nauk. Geom. 1963 (1965) pp. 3–64 (In Russian) |
| [5] | P.A. Shirokov, A.P. Shirokov, "Differentialgeometrie" , Teubner (1962) (Translated from Russian) |
Comments
For the development of affine differential geometry after W. Blaschke, see [a1].
References
| [a1] | U. Simon, "Zur Entwicklung der affine Differentialgeometrie nach Blaschke" , Wilhelm Blaschke gesammelte Werke , 4 , Thales Verlag (1985) pp. 35–88 |
Affine differential geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_differential_geometry&oldid=17614