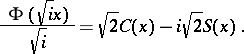The special functions
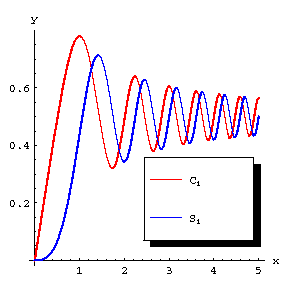
Figure: f041720a
The Fresnel integrals can be represented in the form of the series
An asymptotic representation for large  is:
is:
In a rectangular coordinate system 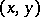 the projections of the curve
the projections of the curve
where 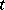 is a real parameter, onto the coordinate planes are the Cornu spiral and the curves
is a real parameter, onto the coordinate planes are the Cornu spiral and the curves 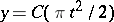 ,
, 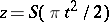 (see Fig. b).
(see Fig. b). 

Figure: f041720b
The generalized Fresnel integrals (see [1]) are functions of the form
The Fresnel integrals are related to the generalized Fresnel integrals as follows:
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
A word of warning. There are different normalizations in use for the Fresnel integrals. E.g., in [a3] they are defined as
so that
The Fresnel integrals defined in the article are related to the probability integral for a complex argument 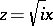 ,
,
(integration along the line 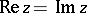 ), by
), by
References
| [a1] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [a2] | J. Spanier, K.B. Oldham, "An atlas of functions" , Hemisphere & Springer (1987) pp. Chapt. 39 |
| [a3] | N.N. Lebedev, "Special functions and their applications" , Dover, reprint (1972) pp. 21–33 (Translated from Russian) |
How to Cite This Entry:
Fresnel integrals. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fresnel_integrals&oldid=17583
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article

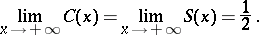


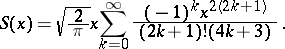
 is:
is:
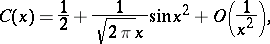
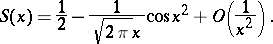
 the projections of the curve
the projections of the curve
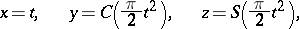
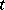 is a real parameter, onto the coordinate planes are the Cornu spiral and the curves
is a real parameter, onto the coordinate planes are the Cornu spiral and the curves 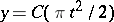 ,
, 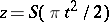 (see Fig. b).
(see Fig. b). 
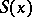
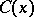



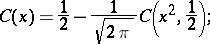
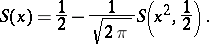
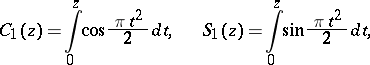
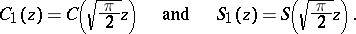
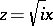 ,
,
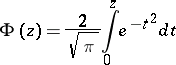
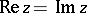 ), by
), by