Fibre product
of a system of topological spaces  with respect to a system of continuous mappings
with respect to a system of continuous mappings  ,
, 
The subset  of the Tikhonov product
of the Tikhonov product  , which is considered in the induced topology and which consists of the points
, which is considered in the induced topology and which consists of the points  for which
for which  , for all indices
, for all indices  and
and  from
from  . The mapping which brings the point
. The mapping which brings the point 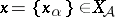 into correspondence with the point
into correspondence with the point  (or with the point
(or with the point  ) is called a projection of the fibre product
) is called a projection of the fibre product  onto
onto  ,
,  (or onto
(or onto  ). If the space
). If the space  is a one-point space, then
is a one-point space, then  . If the
. If the  ,
,  , are completely-regular spaces, the fibre product
, are completely-regular spaces, the fibre product  is completely regular. The fibre product, in particular its special case the partial product, is well suited for the construction of universal (in the sense of homeomorphic inclusion) topological spaces of given weight and given dimension (cf. Universal space).
is completely regular. The fibre product, in particular its special case the partial product, is well suited for the construction of universal (in the sense of homeomorphic inclusion) topological spaces of given weight and given dimension (cf. Universal space).
Comments
In category theory the term "pullbackpullback" is also used, cf. Fibre product of objects in a category.
Fibre product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fibre_product&oldid=17578