Transitive group
A permutation group 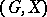 such that each element
such that each element 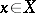 can be taken to any element
can be taken to any element 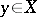 by a suitable element
by a suitable element 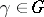 , that is,
, that is, 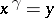 . In other words,
. In other words, 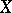 is the unique orbit of the group
is the unique orbit of the group 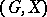 . If the number of orbits is greater than 1, then
. If the number of orbits is greater than 1, then 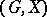 is said to be intransitive. The orbits of an intransitive group are sometimes called its domains of transitivity. For an intransitive group
is said to be intransitive. The orbits of an intransitive group are sometimes called its domains of transitivity. For an intransitive group 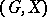 with orbits
with orbits 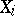 ,
,
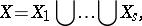 |
and the restriction of the group action to 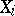 is transitive.
is transitive.
Let 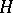 be a subgroup of a group
be a subgroup of a group 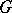 and let
and let
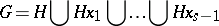 |
be the decomposition of 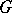 into right cosets with respect to
into right cosets with respect to 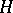 . Further, let
. Further, let 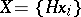 . Then the action of
. Then the action of 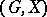 is defined by
is defined by 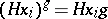 . This action is transitive and, conversely, every transitive action is of the above type for a suitable subgroup
. This action is transitive and, conversely, every transitive action is of the above type for a suitable subgroup 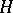 of
of 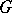 .
.
An action  is said to be
is said to be 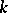 -transitive,
-transitive, 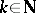 , if for any two ordered sets of
, if for any two ordered sets of 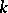 distinct elements
distinct elements 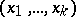 and
and 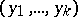 ,
, 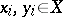 , there exists an element
, there exists an element 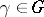 such that
such that 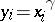 for all
for all 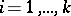 . In other words,
. In other words, 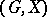 possesses just one anti-reflexive
possesses just one anti-reflexive 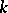 -orbit. For
-orbit. For 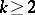 , a
, a 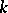 -transitive group is called multiply transitive. An example of a doubly-transitive group is the group of affine transformations
-transitive group is called multiply transitive. An example of a doubly-transitive group is the group of affine transformations  ,
, 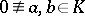 , of some field
, of some field 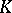 . Examples of triply-transitive groups are the groups of fractional-linear transformations of the projective line over a field
. Examples of triply-transitive groups are the groups of fractional-linear transformations of the projective line over a field 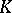 , that is, transformations of the form
, that is, transformations of the form
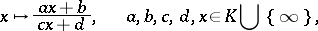 |
where
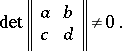 |
A 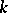 -transitive group
-transitive group  is said to be strictly
is said to be strictly 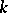 -transitive if only the identity permutation can leave
-transitive if only the identity permutation can leave 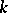 distinct elements of
distinct elements of 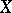 fixed. The group of affine transformations and the group of fractional-linear transformations are examples of strictly doubly- and strictly triply-transitive groups.
fixed. The group of affine transformations and the group of fractional-linear transformations are examples of strictly doubly- and strictly triply-transitive groups.
The finite symmetric group 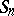 (acting on
(acting on 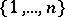 ) is
) is  -transitive. The finite alternating group
-transitive. The finite alternating group 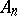 is
is  -transitive. These two series of multiply-transitive groups are the obvious ones. Two
-transitive. These two series of multiply-transitive groups are the obvious ones. Two 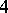 -transitive groups, namely
-transitive groups, namely 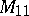 and
and 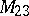 , are known, as well as two
, are known, as well as two  -transitive groups, namely
-transitive groups, namely 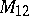 and
and 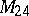 (see [3] and also Mathieu group). There is the conjecture that apart from these four groups there are no non-trivial
(see [3] and also Mathieu group). There is the conjecture that apart from these four groups there are no non-trivial 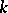 -transitive groups for
-transitive groups for 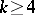 . This conjecture has been proved, using the classification of finite simple non-Abelian groups [6]. Furthermore, using the classification of the finite simple groups, the classification of multiply-transitive groups can be considered complete.
. This conjecture has been proved, using the classification of finite simple non-Abelian groups [6]. Furthermore, using the classification of the finite simple groups, the classification of multiply-transitive groups can be considered complete.
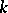 -Transitive groups have also been defined for fractional
-Transitive groups have also been defined for fractional 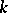 of the form
of the form 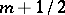 ,
, 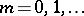 . Namely, a permutation group
. Namely, a permutation group 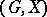 is said to be
is said to be 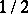 -transitive if either
-transitive if either  , or if all orbits of
, or if all orbits of 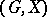 have the same length greater than 1. For
have the same length greater than 1. For 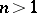 , a group
, a group 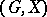 is
is 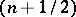 -transitive if the stabilizer
-transitive if the stabilizer 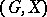 is
is 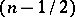 -transitive on
-transitive on 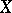 (see [3]).
(see [3]).
References
| [1] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
| [2] | P. Hall, "The theory of groups" , Macmillan (1959) |
| [3] | H. Wielandt, "Finite permutation groups" , Acad. Press (1968) (Translated from German) |
| [4] | D. Passman, "Permutation groups" , Benjamin (1968) |
| [5] | D.G. Higman, "Lecture on permutation representations" , Math. Inst. Univ. Giessen (1977) |
| [6] | P.J. Cameron, "Finite permutation groups and finite simple groups" Bull. London Math. Soc. , 13 (1981) pp. 1–22 |
Comments
The degree of a permutation group  is the number of elements of
is the number of elements of 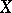 . An (abstract) group
. An (abstract) group 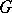 is said to be a
is said to be a 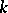 -transitive group if it can be realized as a
-transitive group if it can be realized as a 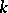 -fold transitive permutation group
-fold transitive permutation group 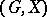 .
.
Due to the classification of finite simple groups, all  -transitive permutation groups have been found. See the list and references in [a1].
-transitive permutation groups have been found. See the list and references in [a1].
An important concept for transitive permutation groups is the permutation rank. It can be defined as the number of orbits of 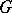 on
on 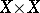 .
.
Primitive permutation groups with permutation rank 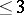 have been almost fully classified by use of the classification of finite simple groups [a2].
have been almost fully classified by use of the classification of finite simple groups [a2].
References
| [a1] | A. Cohen, H. Zantema, "A computation concerning doubly transitive permutation groups" J. Reine Angew. Math. , 347 (1984) pp. 196–211 |
| [a2] | A.E. Brouwer, A.M. Cohen, A. Neumaier, "Distance regular graphs" , Springer (1989) pp. 229 |
Transitive group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transitive_group&oldid=17556