A function describing the influence of particles or groups of particles on one another and the effects due to the interaction of subsystems of the system under consideration.
In classical statistical mechanics, the correlation functions  are defined by the relations
are defined by the relations
where the symbols  in the arguments of the functions denote the sets of coordinates
in the arguments of the functions denote the sets of coordinates  and momenta
and momenta  of the 1st, 2nd
of the 1st, 2nd  particles, respectively, and
particles, respectively, and  are the reduced distribution functions
are the reduced distribution functions
where 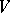 is the volume of the system,
is the volume of the system,  is the number of particles and the
is the number of particles and the  are the distribution functions in the phase space at time
are the distribution functions in the phase space at time 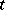 , normalized so that
, normalized so that
The variation of 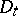 in time is characterized by the Liouville equation
in time is characterized by the Liouville equation 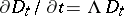 , where
, where 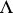 represents the Liouville operator, which is not explicitly dependent on time. One usually considers the case in which
represents the Liouville operator, which is not explicitly dependent on time. One usually considers the case in which  is the sum of an additive part and a binary part characterizing the interactions of the particles:
is the sum of an additive part and a binary part characterizing the interactions of the particles:
According to the principle of correlation damping, the correlation functions satisfy the boundary conditions  as
as  .
.
The correlation functions 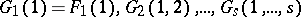 are the functional derivatives,
are the functional derivatives,
of a functional 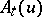 which is related to the so-called generating functional
which is related to the so-called generating functional
by the relation
The functional 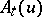 satisfies the equation
satisfies the equation
In quantum statistical mechanics, the correlation functions are operator quantities, defined as follows:
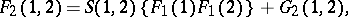 | (*) |
where 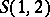 ,
, 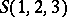 are the symmetrization operator for Bose systems and the anti-symmetrization operator for Fermi systems. The correlation functions (*), forming the density matrix, satisfy the quantum-mechanical Liouville equation (see [2]).
are the symmetrization operator for Bose systems and the anti-symmetrization operator for Fermi systems. The correlation functions (*), forming the density matrix, satisfy the quantum-mechanical Liouville equation (see [2]).
In quantum statistical mechanics, besides the correlation function (*) one considers correlation functions based on conventional thermodynamical averages (see [3]), and correlation functions based on quasi-averages (see [3]).
Bilinear combinations of correlation functions (both quantum-mechanical and classical) yield the Green functions (see [5]). Correlation functions possess spectral representations; they satisfy the Bogolyubov inequality and a variation of the mean-value theorem (see [4]).
Correlation functions corresponding to the Kirkwood decomposition are sometimes used (see [6]); another version is a space-time correlation function (see [8]).
Correlation functions may be interpreted as characteristic functions of probability measures (see [9]).
References
| [1] | N.N. Bogolyubov, "Problems of a dynamical theory in statistical physics" , North-Holland (1962) (Translated from Russian) |
| [2] | N.N. Bogolyubov, K.P. Gurov, Zh. Eksp. i Teoret. Fiziki , 17 : 7 (1947) pp. 614–628 |
| [3] | N.N. Bogolyubov, "Selected works" , 3 , Kiev (1971) (In Russian) |
| [4] | N.N. Bogolyubov jr., B.I. Sadovnikov, "Some questions in statistical mechanics" , Moscow (1975) (In Russian) |
| [5] | N.N. Bogolyubov, S.B. Tyablikov, Dokl. Akad. Nauk SSSR , 159 : 1 (1959) pp. 53–56 |
| [6] | R. Libov, "Introduction to the theory of kinetic equations" , Wiley (1969) |
| [7] | A. Isihara, "Statistical physics" , Acad. Press (1971) |
| [8] | D. Ruelle, "Statistical mechanics: rigorous results" , Benjamin (1974) |
| [9] | C.J. Preston, "Gibbs states on countable sets" , Cambridge Univ. Press (1974) |
How to Cite This Entry:
Correlation function in statistical mechanics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Correlation_function_in_statistical_mechanics&oldid=17541
This article was adapted from an original article by A.N. ErmilovA.M. Kurbatov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article are defined by the relations
are defined by the relations
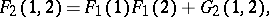
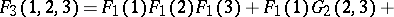

 in the arguments of the functions denote the sets of coordinates
in the arguments of the functions denote the sets of coordinates  and momenta
and momenta  of the 1st, 2nd
of the 1st, 2nd  particles, respectively, and
particles, respectively, and  are the reduced distribution functions
are the reduced distribution functions
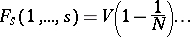
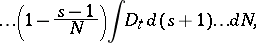
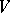 is the volume of the system,
is the volume of the system,  is the number of particles and the
is the number of particles and the  are the distribution functions in the phase space at time
are the distribution functions in the phase space at time 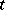 , normalized so that
, normalized so that
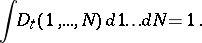
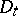 in time is characterized by the Liouville equation
in time is characterized by the Liouville equation 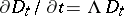 , where
, where 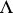 represents the Liouville operator, which is not explicitly dependent on time. One usually considers the case in which
represents the Liouville operator, which is not explicitly dependent on time. One usually considers the case in which  is the sum of an additive part and a binary part characterizing the interactions of the particles:
is the sum of an additive part and a binary part characterizing the interactions of the particles:
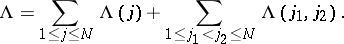
 as
as  .
.
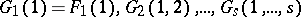 are the functional derivatives,
are the functional derivatives,

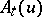 which is related to the so-called generating functional
which is related to the so-called generating functional
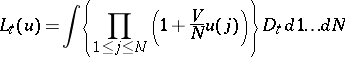
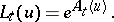
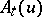 satisfies the equation
satisfies the equation
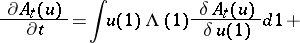
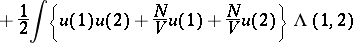
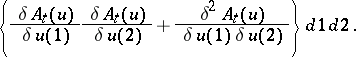
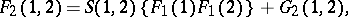

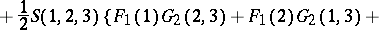

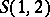 ,
, 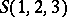 are the symmetrization operator for Bose systems and the anti-symmetrization operator for Fermi systems. The correlation functions (*), forming the density matrix, satisfy the quantum-mechanical Liouville equation (see [2]).
are the symmetrization operator for Bose systems and the anti-symmetrization operator for Fermi systems. The correlation functions (*), forming the density matrix, satisfy the quantum-mechanical Liouville equation (see [2]).