Hilbert theorem

Hilbert's basis theorem. If 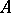is a commutative Noetherian ring and 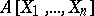is the ring of polynomials in 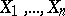with coefficients in 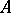, then 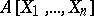is also a Noetherian ring. In particular, in a ring of polynomials in a finite number of variables over a field or over a ring of integers any ideal is generated by a finite number of elements (has a finite basis). This is the form in which the theorem was demonstrated by D. Hilbert [1]; it was used as auxiliary theorem in the proof of Hilbert's theorem on invariants (see below, 8). Subsequently, Hilbert's basis theorem was extensively used in commutative algebra.

References

[1]	D. Hilbert, "Ueber die Theorie der algebraischen Formen" Math. Ann. , 36 (1890) pp. 473–534

V.I. Danilov

Hilbert's irreducibility theorem. Let 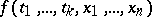be an irreducible polynomial over the field 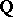of rational numbers; then there exists an infinite set of values 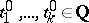of the variables 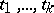for which the polynomial 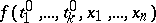is irreducible over 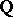. Thus, the polynomial 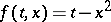remains irreducible for all 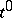(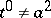, 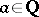) and only for them. This theorem, which was obtained by D. Hilbert in 1892, was subsequently generalized to the case of polynomials over certain other fields (e.g., over a field of finite type over its prime subfield [2]).

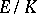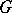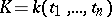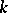Hilbert's irreducibility theorem is employed in investigations connected with the inverse problem in Galois theory and with the arithmetic of algebraic varieties (cf. Galois theory, inverse problem of; Algebraic varieties, arithmetic of). Let there exist an extension with Galois group over the field of rational functions in , with an algebraically closed field in 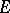such that Hilbert's irreducibility theorem is applicable to it. Then it is possible to choose values of the variables in such that the obtained extension of 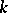has Galois group . With the aid of this concept Hilbert constructed [1] extensions of 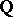with a symmetric and an alternating group; in the case of the symmetric group is taken to be the field of rational functions in variables, while 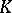is a subfield of the field of symmetric functions, which is itself a field of rational functions. In a generalization of this approach, E. Noether considered an arbitrary subgroup 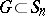and the extension of 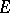of the corresponding field of invariants of 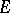with respect to 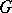[3]. Hilbert's irreducibility theorem makes it possible to construct an extension of 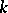with Galois group 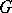, as long as 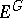is a field of rational functions over 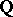. The problem of satisfying this condition (Noether's problem) is closely connected with the Lüroth problem. Only in 1969 was it shown by R. Swan that the answer to the problem is negative in most cases [4], [6].

Hilbert's irreducibility theorem is also employed in constructing rational points of Abelian varieties 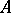over the field 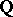of rational numbers. By the Mordell–Weil theorem, the group of rational points of 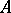is finitely generated and there arises the question of the value of its rank . Using Hilbert's irreducibility theorem, A. Neron constructed varieties 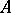of dimension 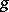and rank higher than or equal to 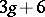[2].

References

[1]	D. Hilbert, "Ueber die Irreducibilität ganzer rationaler Funktionen mit ganzzahligen Koefficienten" J. Reine Angew. Math. , 110 (1892) pp. 104–129
[2]	S. Lang, "Diophantine geometry" , Interscience (1962)
[3]	N.G. Chebotarev, "Galois theory" , Moscow-Leningrad (1936) pp. 18–32 (In Russian)
[4]	J. Martinet, "Un contre-exemple à une conjecture d'E. Noether (d'apres R. Swan)" , Sem. Bourbaki , 22 : 372 (1969–1970)
[5]	A. Schinzel, "Reducibility of polynomials" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 491–496
[6]	V.E. Voskresenskii, "The geometry of linear algebraic groups" Proc. Steklov Inst. Math. , 132 (1975) pp. 178–183 Trudy Mat. Inst. Steklov. , 132 (1973) pp. 151–161

A.N. Parshin

Hilbert's Nullstellen Satz, Hilbert's zero theorem, Hilbert's root theorem. Let 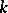be a field, let 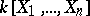be a ring of polynomials over , let 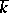be the algebraic closure of 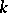, and let 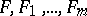be polynomials in 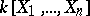. A root of the polynomial 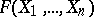is a sequence 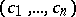of elements in 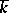satisfying the condition 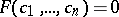. If each common root of the polynomials 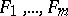is a root of the polynomial 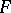, then there exists an integer , depending only on , such that 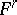belongs to the ideal generated by 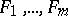, i.e.

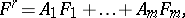where 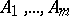are certain polynomials. This result has been obtained by D. Hilbert [1].

The theorem is equivalent to the statement that for any proper ideal of the ring 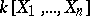there exists a root which is common to all polynomials in . Thus, this theorem may be regarded as a far-reaching generalization of the fundamental theorem of algebra (cf. Algebra, fundamental theorem of). It may also be regarded as the statement that any prime ideal of the ring 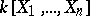is the intersection of the maximal ideals which contain it; this leads to the concept of a Jacobson ring.

In the geometric interpretation, the roots of an ideal 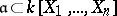correspond to the algebraic points of the affine variety defined by . Hilbert's theorem implies that there exists an algebraic point in any non-empty affine variety. Thus, the set of algebraic points is everywhere dense on the variety and thus uniquely defines it — which is the reason why one often restricts oneself to algebraic points when studying algebraic varieties.

References

[1]	D. Hilbert, "Ueber die vollen Invariantensysteme" Math. Ann. , 42 (1893) pp. 313–373
[2]	B.L. van der Waerden, "Algebra" , 2 , Springer (1971) (Translated from German)
[3]	O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975)
[4]	S. Lang, "Algebra" , Addison-Wesley (1974)
[5]	N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)

V.I. Danilov

Hilbert's theorem on surfaces of negative curvature. In the three-dimensional Euclidean space there is no complete regular surface of constant negative curvature. Demonstrated by D. Hilbert [1] in 1901.

References

[1]	D. Hilbert, "Grundlagen der Geometrie" , Springer (1913)

E.V. Shikin

Hilbert's syzygies theorem. A theorem on finiteness of a syzygies chain (cf. Syzygy) of a graded module over a ring of polynomials (for the classical formulation see [1]).

Let 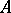be a Noetherian ring, let be a Noetherian 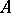-module and let be a system of generators of 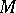. The module of syzygies (relations) 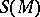of 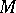is the module of relations for , i.e. the 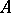-module of vectors 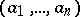, , 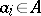which satisfy the condition 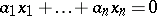. Inductively one defines the 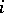-th module of syzygies by 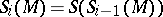(where 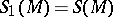). It may also be described in a different manner as an exact sequence, known as a chain of syzygies:

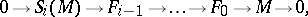where 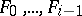are free 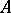-modules of finite type. In its modern interpretation, Hilbert's syzygies theorem is formulated as follows: If 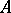is a local regular ring of dimension 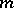, the -th module of syzygies of an arbitrary Noetherian 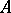-module is a free module. This is equivalent to saying that any 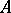-module has a free resolution of length 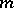or that has global projective dimension 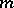. This property is characteristic of regular rings [2].

The global variant of Hilbert's syzygies theorem: Over a regular ring 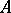(e.g. over a ring of polynomials) any 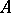-module of finite type has a projective (but not necessarily free) resolution of finite length.

References

[1]	D. Hilbert, "Ueber die Theorie der algebraischen Formen" Math. Ann. , 36 (1890) pp. 473–534
[2]	J.-P. Serre, "Sur la dimension homologique des anneaux et des modules noethériens" S. Iyanaga (ed.) Y. Kawada (ed.) , Proc. Internat. Symp. Algebraic Number Theory , Sci. Council Tokyo (1955) pp. 175–189
[3]	J.-P. Serre, "Algèbre locale. Multiplicités" , Lect. notes in math. , 11 , Springer (1965)
[4]	O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975)

V.I. Danilov

Hilbert's theorem on cyclic extensions (Hilbert's theorem 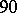). Let be a cyclic extension of a field with cyclic Galois group 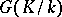and let 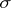be the generator of 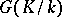; the norm of an element 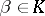is then equal to one if and only if there exists a non-zero element 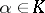satisfying the condition 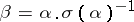. In a similar manner, the trace 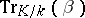is zero if and only if 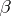can be represented in the form 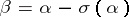, , 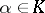[1], [2], [3].

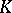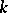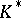Hilbert's theorem may be considered as a consequence of a more general theorem on the cohomology of Galois groups [4]. In fact, if is a Galois extension of a field with Galois group , then the multiplicative group of 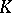has the structure of a 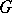-module, and the first cohomology group 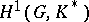vanishes. In the same manner, if 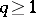, 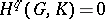(cf. Galois cohomology).

Another generalization of Hilbert's theorem is Grothendieck's descent theorem; one of its applications in étale topology, which is also known as Hilbert's theorem 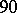, states that the étale cohomology groups of a scheme 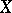with values in a sheaf of multiplicative groups 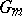is isomorphic to the Picard group 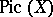of classes of invertible sheafs on [5].

References

[1]	D. Hilbert, "Die Theorie der algebraischen Zahlkörper" Jahresber. Deutsch. Math.-Verein , 4 (1897) pp. 175–546
[2]	S. Lang, "Algebra" , Addison-Wesley (1974)
[3]	N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French)
[4]	J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964)
[5]	M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , Théorie des topos et cohomologie étale des schémas (SGA 4) , Lect. notes in math. , 269; 270; 305 , Springer (1972–1973)

V.I. Danilov

Hilbert's theorem on the existence of an absolute extremum: Let

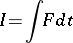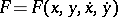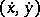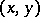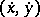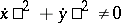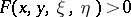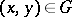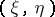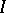be the functional of a variational problem in parametric form, where is a positive-definite function of the first degree in which is three times continuously differentiable with respect to all arguments for all from a domain and all which meet the condition . It also assumed that for all and all with (i.e. the functional is positive definite), and also that the sets 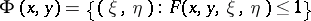are strictly convex with respect to 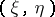for all 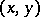in a closed convex subdomain 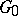(i.e. the functional 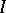is regular or elliptic).

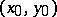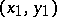Under the above assumptions it is possible to find for any two points and in 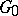a curve which is the absolute minimum over all rectifiable curves for .

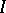The theorem was obtained by D. Hilbert in 1899.

References

[1]	N.I. Akhiezer, "The calculus of variations" , Blaisdell (1962) (Translated from Russian)

V.M. Tikhomirov

Hilbert's theorem on invariants. A theorem that establishes that the algebra of all polynomials on the complex vector space of forms of degree in variables which are invariant with respect to the action of the general linear group 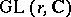, defined by linear substitutions of these variables, is finitely generated. The first proof of the theorem using Hilbert's basis theorem as well as formal processes of the theory of invariants, was given in [1] (cf. also Invariants, theory of). D. Hilbert [2] gave a constructive proof of this theorem.

Hilbert's theorem is the first fundamental theorem of the theory of invariants for the 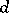-th symmetric degree of the standard representation of 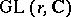. The proof of Hilbert's theorem stimulated the formulation of the problem of finite generation of algebras of invariants for subgroups of 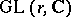and also the formulation of Hilbert's 14th problem. It was proved by H. Weyl, who employed the theory of integration on groups, that the algebra of invariants is finitely generated for any finite-dimensional representation of a compact Lie group or a complex semi-simple Lie group [3].

Hilbert's theorem is also the name usually given to the following generalization. If 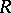is an algebra of finite type over a field 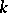, if 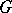is the geometrically reductive group of its 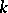-automorphisms and if is the subalgebra of all 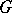-invariant elements in 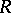, then 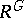is also of finite type over 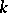[4], [5].

References

[1]	D. Hilbert, "Ueber die Theorie der algebraischen Formen" Math. Ann. , 36 (1890) pp. 473–534
[2]	D. Hilbert, "Ueber die vollen Invariantensysteme" Math. Ann. , 42 (1893) pp. 313–373
[3]	H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946)
[4]	D. Mumford, "Geometric invariant theory" , Springer (1965)
[5]	M. Nagata, "Invariants of a group in an affine ring" J. Math. Kyoto Univ. , 3 (1964) pp. 369–377