Additive relation

A submodule of the direct sum of two modules and over some ring . An additive relation can thus be regarded also as a (not necessary single-valued) mapping or, more exactly, as a "many-valued" homomorphism, i.e. a homomorphism of the submodule into the quotient module where

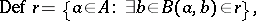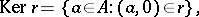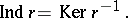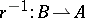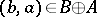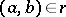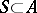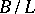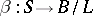Here, is the relation inverse to ; it consists of all pairs such that . Conversely, if a submodule , a quotient module of the module and a homomorphism are given, then there also exists a unique additive relation such that .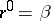

If two additive relations and 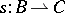are given, then, as in the case of other binary relations, it is possible to define their product, , which is the set of all pairs 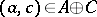such that there exists an element 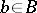for which 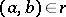and . This multiplication is associative (wherever defined) and, moreover, the additive relations form a category with involution .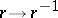

Additive relations are used in natural definitions of connecting homomorphisms for exact sequences of complexes. The above considerations are valid not only in the category of modules, but also in any other Abelian category.

References

[1]	S. MacLane, "Homology" , Springer (1963)
[2]	D. Puppe, "Korrespondenzen in Abelschen Kategorien" Math. Ann , 148 (1962) pp. 1–30