Parabolic subalgebra
A subalgebra of a finite-dimensional Lie algebra 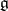 over an algebraically closed field that contains a Borel subalgebra, i.e. a maximal solvable subalgebra of
over an algebraically closed field that contains a Borel subalgebra, i.e. a maximal solvable subalgebra of  (cf. also Lie algebra, solvable). If
(cf. also Lie algebra, solvable). If  is a finite-dimensional Lie algebra over an arbitrary field
is a finite-dimensional Lie algebra over an arbitrary field  , then a subalgebra
, then a subalgebra  of it is also called a parabolic subalgebra if
of it is also called a parabolic subalgebra if  is a parabolic subalgebra of
is a parabolic subalgebra of  , where
, where  is the algebraic closure of the field
is the algebraic closure of the field 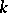 . If
. If 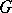 is an irreducible linear algebraic group over a field of characteristic 0 and
is an irreducible linear algebraic group over a field of characteristic 0 and 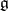 is its Lie algebra, then a subalgebra
is its Lie algebra, then a subalgebra 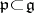 is a parabolic subalgebra in
is a parabolic subalgebra in  if and only if it coincides with the Lie algebra of some parabolic subgroup of
if and only if it coincides with the Lie algebra of some parabolic subgroup of 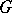 .
.
Examples of parabolic subalgebras in the Lie algebra of all square matrices of order  over a field
over a field 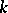 are the subalgebras of type
are the subalgebras of type 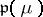 (
(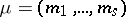 is an arbitrary set of natural numbers with sum equal to
is an arbitrary set of natural numbers with sum equal to  ), where the algebra
), where the algebra 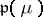 consists of all upper-triangular block-diagonal matrices with as diagonal blocks square matrices of orders
consists of all upper-triangular block-diagonal matrices with as diagonal blocks square matrices of orders  .
.
Let 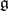 be a reductive finite-dimensional Lie algebra (cf. Lie algebra, reductive) over a field
be a reductive finite-dimensional Lie algebra (cf. Lie algebra, reductive) over a field 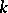 of characteristic 0, let
of characteristic 0, let 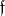 be a maximal diagonalizable subalgebra of
be a maximal diagonalizable subalgebra of 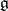 over
over 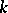 , let
, let 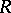 be the system of
be the system of 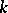 -roots of
-roots of 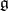 relative to
relative to 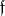 (cf. Root system), let
(cf. Root system), let 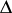 be a basis (a set of simple roots) of
be a basis (a set of simple roots) of 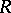 , and let
, and let 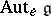 be the group of elementary automorphisms of
be the group of elementary automorphisms of  , i.e. the group generated by the automorphisms of the form
, i.e. the group generated by the automorphisms of the form 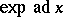 , where
, where  is a nilpotent element of
is a nilpotent element of 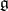 . Then every parabolic subalgebra of the Lie algebra
. Then every parabolic subalgebra of the Lie algebra 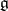 is transformed by some automorphism from
is transformed by some automorphism from 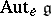 into one of the standard parabolic subalgebras of the type
into one of the standard parabolic subalgebras of the type
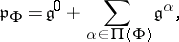 |
where 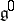 is the centralizer of the subalgebra
is the centralizer of the subalgebra 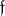 in
in 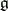 ,
, 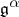 is the root subspace of the Lie algebra
is the root subspace of the Lie algebra 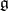 corresponding to the root
corresponding to the root 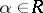 ,
, 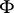 is an arbitrary subset of the set
is an arbitrary subset of the set 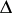 , and
, and 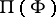 is the set of those roots in
is the set of those roots in 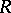 whose decomposition into the sum of simple roots from
whose decomposition into the sum of simple roots from 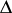 contains elements of
contains elements of  only with non-negative coefficients. In this way the number of classes of parabolic subalgebras conjugate with respect to
only with non-negative coefficients. In this way the number of classes of parabolic subalgebras conjugate with respect to 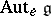 turns out to be
turns out to be 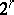 , where
, where 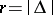 is the
is the 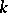 -rank of the semi-simple Lie algebra
-rank of the semi-simple Lie algebra 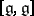 . In addition, if
. In addition, if  , then
, then 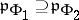 . In particular,
. In particular, 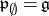 , and
, and 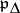 is the minimal parabolic subalgebra of
is the minimal parabolic subalgebra of 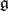 .
.
All non-reductive maximal subalgebras of finite-dimensional reductive Lie algebras over a field of characteristic 0 are parabolic subalgebras (see [2], [3], [5]).
References
| [1] | N. Bourbaki, "Groupes et algèbres de Lie" , Hermann (1975) pp. Chapts. VII-VIII |
| [2] | F.I. Karpelevich, "On non-semi-simple maximal subalgebras of semi-simple Lie algebras" Dokl. Akad. Nauk USSR , 76 (1951) pp. 775–778 (In Russian) |
| [3] | V.V. Morozov, "Proof of the regularity theorem" Uspekhi Mat. Nauk , 11 (1956) pp. 191–194 (In Russian) |
| [4] | G.D. Mostow, "On maximal subgroups of real Lie groups" Ann. of Math. , 74 (1961) pp. 503–517 |
| [5] | A. Borel, J. Tits, "Eléments unipotents et sous-groupes paraboliques de groupes réductifs I" Invent. Math. , 12 (1971) pp. 95–104 |
Parabolic subalgebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_subalgebra&oldid=17501