Lagrange interpolation formula
A formula for obtaining a polynomial of degree  (the Lagrange interpolation polynomial) that interpolates a given function
(the Lagrange interpolation polynomial) that interpolates a given function  at nodes
at nodes  :
:
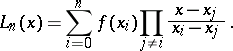 | (1) |
When the  are equidistant, that is,
are equidistant, that is,  , using the notation
, using the notation  one can reduce (1) to the form
one can reduce (1) to the form
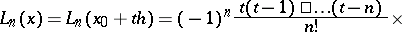 | (2) |
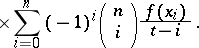 |
In the expression (2), called the Lagrange interpolation formula for equidistant nodes, the coefficients
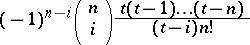 |
of the 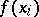 are called the Lagrange coefficients.
are called the Lagrange coefficients.
If 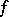 has a derivative of order
has a derivative of order 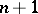 on the interval
on the interval 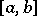 , if all interpolation nodes lie in this interval and if for any point
, if all interpolation nodes lie in this interval and if for any point 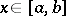 one defines
one defines
 |
then a point 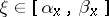 exists such that
exists such that
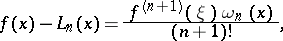 |
where
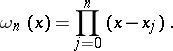 |
If the absolute value of the derivative 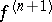 is bounded on
is bounded on 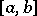 by a constant
by a constant 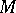 and if the interpolation nodes are chosen such that the roots of the Chebyshev polynomial of degree
and if the interpolation nodes are chosen such that the roots of the Chebyshev polynomial of degree 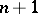 are mapped into these points under a linear mapping from
are mapped into these points under a linear mapping from  onto
onto  , then for any
, then for any 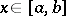 one has
one has
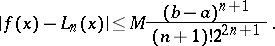 |
If the interpolation nodes are complex numbers  and lie in some domain
and lie in some domain  bounded by a piecewise-smooth contour
bounded by a piecewise-smooth contour 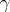 , and if
, and if 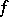 is a single-valued analytic function defined on the closure of
is a single-valued analytic function defined on the closure of 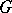 , then the Lagrange interpolation formula has the form
, then the Lagrange interpolation formula has the form
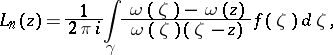 |
where
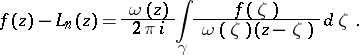 |
The Lagrange interpolation formula for interpolation by means of trigonometric polynomials is:
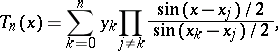 |
which is a trigonometric polynomial of order  having prescribed values
having prescribed values  at the given nodes
at the given nodes  .
.
The formula was proposed by J.L. Lagrange in 1795.
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
Comments
References
| [a1] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126 |
| [a2] | L.W. Johnson, R.D. Riess, "Numerical analysis" , Addison-Wesley (1977) |
| [a3] | G.M. Phillips, P.J. Taylor, "Theory and applications of numerical analysis" , Acad. Press (1973) |
Lagrange interpolation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lagrange_interpolation_formula&oldid=17497