Queue, multi-channel with waiting
multi-server queue
A queue for which the algorithm provides for the calls to form a queue if the system is busy at the time of their arrival; here the service of calls takes place in several channels simultaneously. The basic definitions and notations are as in Queue.
The operation of a multi-server queue, controlled by a sequence 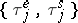 , is as follows. Calls arrive at times
, is as follows. Calls arrive at times 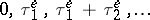 . A time
. A time  is spent on the service of the
is spent on the service of the 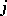 -th call, no matter which of the
-th call, no matter which of the 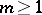 channels serves the call. Calls arrive and are immediately directed (in order of arrival) to a free channel if not all channels are busy, or wait until some channel is free and then proceed into service. For simplicity, let the system be free at time
channels serves the call. Calls arrive and are immediately directed (in order of arrival) to a free channel if not all channels are busy, or wait until some channel is free and then proceed into service. For simplicity, let the system be free at time 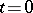 .
.
1) For clarity of exposition the following notation is used: 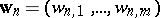 is the vector of waiting times of the
is the vector of waiting times of the  -th call, where
-th call, where 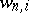 is the time this call must wait until
is the time this call must wait until 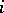 channels are free of calls which arrived before it, so
channels are free of calls which arrived before it, so 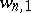 is the "actual" waiting time. In addition, let
is the "actual" waiting time. In addition, let 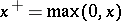 ,
,
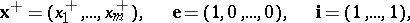 |
and let 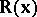 be the vector obtained from
be the vector obtained from  by placing the coordinates in increasing order (so the first coordinate of
by placing the coordinates in increasing order (so the first coordinate of  is
is  ). Then the following recurrence relation holds for
). Then the following recurrence relation holds for  , generalizing the one-dimensional case:
, generalizing the one-dimensional case:
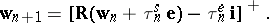 | (1) |
If 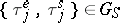 and
and 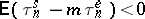 , then there is a proper sequence
, then there is a proper sequence 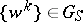 which satisfies (1) and is such that the distribution function of
which satisfies (1) and is such that the distribution function of 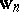 converges monotone to the distribution function of
converges monotone to the distribution function of  as
as 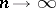 . This result has a generalization to the case
. This result has a generalization to the case 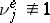 and can also be extended to the queue length
and can also be extended to the queue length  at the time of arrival of the
at the time of arrival of the  -th call (
-th call (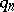 is the queue length excluding calls in service). There are formulas connecting the limit distributions of
is the queue length excluding calls in service). There are formulas connecting the limit distributions of 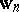 and
and 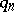 .
.
If 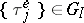 ,
, 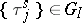 , then (1) allows one to write an integral equation for the stationary distribution of
, then (1) allows one to write an integral equation for the stationary distribution of 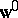 . In this case it is possible to also give simple relations between the stationary distribution of the queue length and the waiting time. Specifically, if
. In this case it is possible to also give simple relations between the stationary distribution of the queue length and the waiting time. Specifically, if 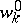 denotes the
denotes the 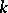 -th coordinate of the vector
-th coordinate of the vector 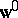 , then for
, then for  ,
,
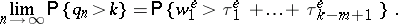 |
If 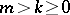 , then
, then
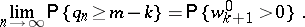 |
Here, all random variables under the probability sign are independent.
If, in addition, 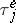 has a non-lattice distribution, similar formulas are true for the limit distribution of
has a non-lattice distribution, similar formulas are true for the limit distribution of 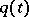 . If
. If 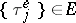 , then
, then
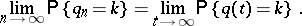 |
2) If 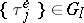 ,
, 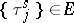 , then it is possible to give explicit formulas for the limit distribution of
, then it is possible to give explicit formulas for the limit distribution of 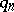 ,
, 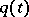 and
and 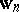 . Let
. Let  be the index of the distribution of
be the index of the distribution of 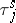 and let
and let 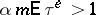 . Then the numbers
. Then the numbers
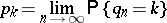 |
can be described explicitly by rational functions of the values 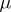 and
and  ,
, 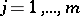 , where
, where 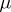 is the unique root in
is the unique root in 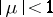 of the equation
of the equation
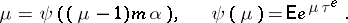 |
If  , then
, then
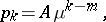 |
where  does not depend on
does not depend on  . For the limit distribution of the waiting time,
. For the limit distribution of the waiting time,
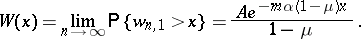 |
If  is a non-lattice random variable, then
is a non-lattice random variable, then
 |
exists, where
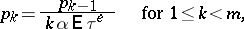 |
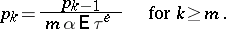 |
In case  ,
, 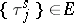 ,
,
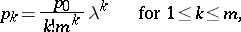 |
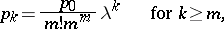 |
where
 |
3) Stability theorems (about the continuous dependence of the stationary distributions of  on the distributions of
on the distributions of 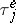 and
and 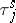 ) are obtained in a less general form than for single-server systems, and are connected with a condition on the existence of so-called renewal events. However, in case
) are obtained in a less general form than for single-server systems, and are connected with a condition on the existence of so-called renewal events. However, in case 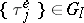 ,
,  , the condition
, the condition 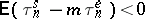 , must be satisfied. If for such systems, in triangular arrays, the distributions of
, must be satisfied. If for such systems, in triangular arrays, the distributions of 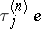 and
and 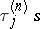 converge weakly to the distributions of
converge weakly to the distributions of  and
and 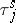 , respectively, and, in addition,
, respectively, and, in addition,  , then the distribution of
, then the distribution of 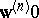 will converge weakly to the distribution of
will converge weakly to the distribution of  .
.
4) Asymptotic methods used in the analysis of multi-server systems with heavy traffic give results similar to the corresponding results for single-server systems.
In a series of control sequences 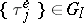 ,
, 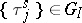 , let
, let
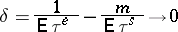 |
(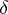 is the difference between the mean number of calls joining the system and the mean number of calls which the system can serve in unit time: if
is the difference between the mean number of calls joining the system and the mean number of calls which the system can serve in unit time: if 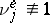 ,
,  , then
, then  can be taken to be the number
can be taken to be the number 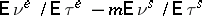 , which has the same meaning). Now if
, which has the same meaning). Now if
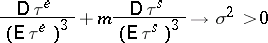 |
and 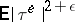 ,
,  are uniformly bounded for some
are uniformly bounded for some 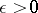 , then the following holds as
, then the following holds as 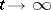 ,
, 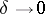 for the queue length
for the queue length  at time
at time 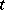 :
:
for 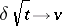 ,
, 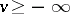 ,
,
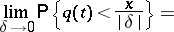 |
 |
where  is a standard Wiener process;
is a standard Wiener process;
for 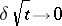 ,
,
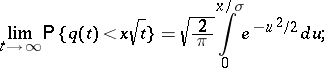 |
for 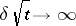 ,
, 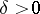 ,
,
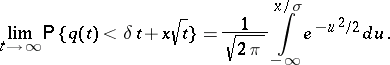 |
Similar relations are true for the queue length 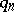 and the waiting time
and the waiting time 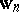 .
.
Another possible direction for asymptotic investigation of multi-server systems is the study of systems with intensive input stream and an unboundedly increasing (with 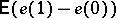 ) number of service channels.
) number of service channels.
5) The behaviour of multi-server systems with an infinite number of service channels and with a control sequence 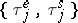 is described in the same way as the behaviour of multi-server systems with waiting; the only difference being that here there is always a free channel and, consequently, the waiting time for any call is equal to zero. As a characteristic of the state of the system one takes the number of busy lines
is described in the same way as the behaviour of multi-server systems with waiting; the only difference being that here there is always a free channel and, consequently, the waiting time for any call is equal to zero. As a characteristic of the state of the system one takes the number of busy lines 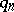 at the time of arrival of the
at the time of arrival of the  -th call or the number
-th call or the number 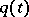 of busy lines at time
of busy lines at time  (as everywhere above,
(as everywhere above,  and
and 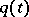 are the queue lengths and
are the queue lengths and 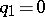 ).
).
Let 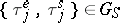 and, in addition, let
and, in addition, let 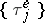 be metrically transitive. Then, if
be metrically transitive. Then, if  , the distribution of the sequence
, the distribution of the sequence 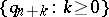 converges monotone, as
converges monotone, as 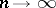 , to the distribution of the strictly stationary sequence
, to the distribution of the strictly stationary sequence
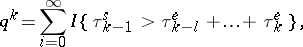 | (2) |
where 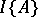 is the indicator of the event
is the indicator of the event 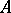 . The condition
. The condition 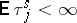 is nearly a necessary condition for the finiteness of (2).
is nearly a necessary condition for the finiteness of (2).
6) For systems in which  ,
, 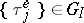 ,
, 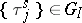 , the distribution of the stationary queue length
, the distribution of the stationary queue length  can be described with the help of equations. For this, one introduces the variable
can be described with the help of equations. For this, one introduces the variable
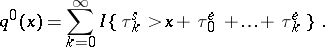 |
The number 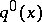 indicates how many calls are in the system operating in a stationary regime, if one goes back to a time
indicates how many calls are in the system operating in a stationary regime, if one goes back to a time  after the arrival of a certain call but not counting that call and the calls arriving after it.
after the arrival of a certain call but not counting that call and the calls arriving after it.
Denoting
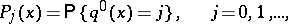 |
 |
one obtains
 |
the system of functions  satisfies the equations
satisfies the equations
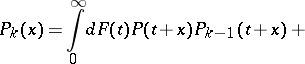 |
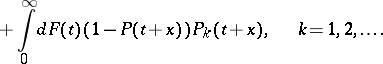 |
Here 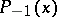 must be equal to
must be equal to  . Each of the first
. Each of the first 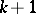 equations of this system, relative to
equations of this system, relative to 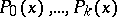 , has a unique solution in the class of functions of bounded variation with the properties
, has a unique solution in the class of functions of bounded variation with the properties
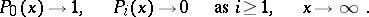 |
Similar results hold for the distribution of 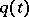 . If
. If 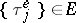 ,
, 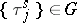 , then
, then
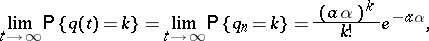 |
where 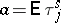 and
and 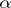 is the exponent of the distribution of
is the exponent of the distribution of 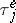 .
.
If 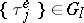 ,
, 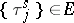 , then
, then
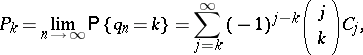 |
where
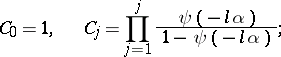 |
 |
and  is the exponent of the distribution of
is the exponent of the distribution of 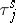 . If, in addition,
. If, in addition, 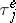 is a non-lattice random variable, then
is a non-lattice random variable, then
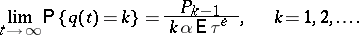 |
7) Stability theorems in the case 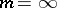 , as in the preceding sections, give conditions under which a small change in the control sequences leads to a small change in the stationary distribution of the number
, as in the preceding sections, give conditions under which a small change in the control sequences leads to a small change in the stationary distribution of the number 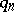 of busy lines.
of busy lines.
For triangular arrays, when the system is controlled by a stationary sequence 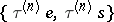 depending on a parameter
depending on a parameter 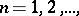 let the following conditions hold.
let the following conditions hold.
A) There is a sequence 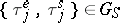 such that
such that 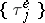 is metrically transitive,
is metrically transitive, 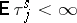 and the finite-dimensional distributions of
and the finite-dimensional distributions of 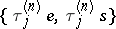 converge to the distributions of
converge to the distributions of 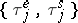 as
as  .
.
B)  as
as 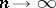 .
.
C) The distributions of  for all
for all 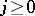 are continuous at the point
are continuous at the point  .
.
The stability theorem then asserts that under conditions A)–C) the distributions of the sequence 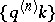 of queue lengths (defined by (2) with respect to the control sequence
of queue lengths (defined by (2) with respect to the control sequence 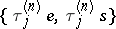 ) converge to the distributions of
) converge to the distributions of 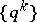 as
as 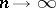 .
.
All three conditions A), B) and C) in this result are essential; the failure of any one of these immediately allows the construction of examples where the distributions of 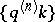 do not converge.
do not converge.
8) Asymptotic analysis of systems with an infinite number of service channels is natural and effective in the study of so-called traffic systems, when the input stream has high intensity. The advantage of the asymptotic approach lies in the great generality and universality of the laws established.
Let the input stream  , denoting the number of calls arriving in the system up to time
, denoting the number of calls arriving in the system up to time 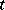 , depend on a parameter
, depend on a parameter 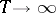 (a triangular array), so that
(a triangular array), so that 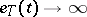 as
as 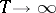 for each fixed
for each fixed 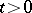 and, in addition, let there exist a non-decreasing function
and, in addition, let there exist a non-decreasing function  , a function
, a function 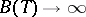 as
as 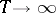 and a continuous random process
and a continuous random process 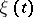 , defined on
, defined on 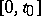 , such that the distribution of
, such that the distribution of 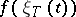 , where
, where
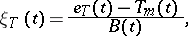 |
converges weakly to the distribution of 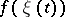 as
as 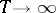 , for any functional
, for any functional  which is measurable and continuous in the uniform metric.
which is measurable and continuous in the uniform metric.
For example, if 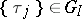 and if the control of the system is via a sequence
and if the control of the system is via a sequence 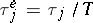 , then the condition stated will be satisfied for any
, then the condition stated will be satisfied for any  , where
, where
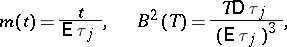 |
and  is a standard Wiener process.
is a standard Wiener process.
Regarding the service mechanism it is assumed that  . Then:
. Then:
a) If 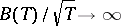 , then the finite-dimensional distributions of the normalized queue
, then the finite-dimensional distributions of the normalized queue
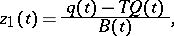 |
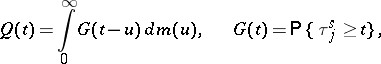 |
converge weakly as 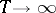 to the distributions of the process
to the distributions of the process
 |
b) If 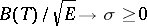 , then the finite-dimensional distributions of the process
, then the finite-dimensional distributions of the process
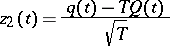 |
converge weakly to the finite-dimensional distributions of the process
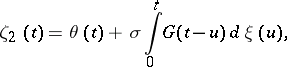 |
where 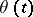 is a centred Gaussian process not depending on
is a centred Gaussian process not depending on  with covariance function
with covariance function
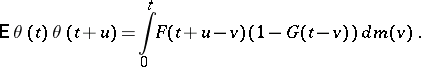 |
If the functions  or
or 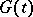 are required to have some degree of smoothness, then the convergence of
are required to have some degree of smoothness, then the convergence of  to
to  ,
,  , holds even in a stronger sense (for example, convergence of the distribution of
, holds even in a stronger sense (for example, convergence of the distribution of 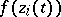 to that of
to that of  as
as  for all functionals continuous relative to the uniform metric).
for all functionals continuous relative to the uniform metric).
For references see Queueing theory.
Queue, multi-channel with waiting. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Queue,_multi-channel_with_waiting&oldid=17489