Bunyakovskii conjecture
Let  be a polynomial of degree
be a polynomial of degree  with integer coefficients. Already in 1854, V. Bunyakovskii [a1] considered the problem whether
with integer coefficients. Already in 1854, V. Bunyakovskii [a1] considered the problem whether  represents infinitely many prime numbers as
represents infinitely many prime numbers as  ranges over the positive integers (cf. Prime number). There are some obvious necessary conditions, e.g., that the coefficients of
ranges over the positive integers (cf. Prime number). There are some obvious necessary conditions, e.g., that the coefficients of  are relatively prime, that
are relatively prime, that  is irreducible (cf. Irreducible polynomial) and, trivially, that the leading coefficient is positive. Are these conditions sufficient?
is irreducible (cf. Irreducible polynomial) and, trivially, that the leading coefficient is positive. Are these conditions sufficient?
As Bunyakovskii remarked, the answer is "no" . For instance, for each prime number  one has
one has
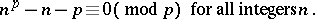 |
Replacing the constant term  by
by 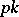 with a suitable integer
with a suitable integer  , one can make
, one can make 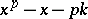 irreducible, say with
irreducible, say with  ,
, 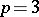 , etc. Hence, one has to assume that the values
, etc. Hence, one has to assume that the values 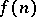 for positive integers
for positive integers  are not all divisible by a prime number. Bunyakovskii's conjecture is that these conditions are sufficient.
are not all divisible by a prime number. Bunyakovskii's conjecture is that these conditions are sufficient.
A special case of this conjecture is that the polynomial 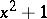 represents infinitely many prime numbers. Similarly, the Dirichlet theorem about infinitely many primes in an arithmetic progression comes from considering the polynomial
represents infinitely many prime numbers. Similarly, the Dirichlet theorem about infinitely many primes in an arithmetic progression comes from considering the polynomial  with relatively prime integers
with relatively prime integers  and
and 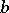 .
.
Bunyakovskii's conjecture was rediscovered and generalized to several polynomials by A. Schinzel [a2]; see also the comments in [a3].
P.T. Bateman and R. Horn have conjectured an asymptotic behaviour (cf. Bateman–Horn conjecture).
References
| [a1] | V. Bouniakowsky [V. Bunyakovskii], "Sur les diviseurs numériques invariables des fonctions rationelles entières" Mém. Sci. Math. et Phys. , VI (1854–1855) pp. 307–329 |
| [a2] | A. Schinzel, W. Sierpiński, "Sur certaines hypothèses concernant les nombres premiers" Acta Arithm. , 4 (1958) pp. 185–208 |
| [a3] | H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974) |
Bunyakovskii conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bunyakovskii_conjecture&oldid=17472