Fine sheaf

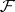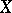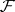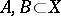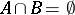A sheaf of Abelian groups over a paracompact space with a soft sheaf as sheaf of endomorphisms. A sheaf is fine if and only if for any closed subsets with there is an endomorphism 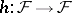that is the identity on 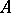and zero on 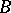, or equivalently if for every open covering 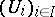of 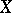there is a locally finite collection 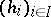of endomorphisms of 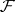such that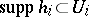 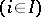and 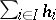is the identity endomorphism. Every fine sheaf is soft, and if 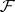is a sheaf of rings with an identity, the converse also holds. If 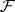is a fine sheaf and is an arbitrary sheaf of Abelian groups, then 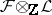is also a fine sheaf. An example of a fine sheaf is the sheaf of germs of continuous (or differentiable of class 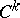) sections of a vector bundle over a paracompact space (respectively, over a paracompact differentiable manifold).

References

[1]	R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958)
[2]	R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)