Brown-Gitler spectra
Spectra introduced by E.H. Brown Jr. and S. Gitler [a1] to study higher-order obstructions to immersions of manifolds (cf. also Immersion; Spectrum of spaces). They immediately found wide applicability in a variety of areas of homotopy theory, most notably in the stable homotopy groups of spheres ([a9] and [a4]), in studying homotopy classes of mappings out of various classifying spaces ([a3], [a10] and [a8]), and, as might be expected, in studying the immersion conjecture for manifolds ([a2] and [a5]).
The modulo- homology
homology  comes equipped with a natural right action of the Steenrod algebra
comes equipped with a natural right action of the Steenrod algebra  which is unstable: at the prime
which is unstable: at the prime  , for example, this means that
, for example, this means that
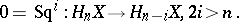 |
Write  for the category of all unstable right modules over
for the category of all unstable right modules over  . This category has enough projective objects; indeed, there is an object
. This category has enough projective objects; indeed, there is an object  ,
,  , of
, of  and a natural isomorphism
and a natural isomorphism
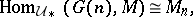 |
where  is the vector spaces of elements of degree
is the vector spaces of elements of degree  in
in 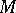 . The module
. The module  can be explicitly calculated. For example, if
can be explicitly calculated. For example, if  and
and  is the universal class, then the evaluation mapping
is the universal class, then the evaluation mapping 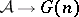 sending
sending  to
to 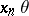 defines an isomorphism
defines an isomorphism
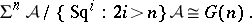 |
These are the dual Brown–Gitler modules.
This pleasant bit of algebra can be only partly reproduced in algebraic topology. For example, for general  there is no space whose (reduced) homology is
there is no space whose (reduced) homology is  ; specifically, if
; specifically, if 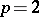 , the module
, the module 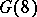 cannot support the structure of an unstable co-algebra over the Steenrod algebra. However, after stabilizing, this objection does not apply and the following result from [a1], [a4], [a6] holds: There is a unique
cannot support the structure of an unstable co-algebra over the Steenrod algebra. However, after stabilizing, this objection does not apply and the following result from [a1], [a4], [a6] holds: There is a unique  -complete spectrum
-complete spectrum 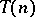 so that
so that  and for all pointed CW-complexes
and for all pointed CW-complexes 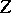 , the mapping
, the mapping
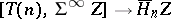 |
sending  to
to 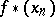 is surjective. Here,
is surjective. Here, 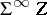 is the suspension spectrum of
is the suspension spectrum of  , the symbol
, the symbol  denotes stable homotopy classes of mappings, and
denotes stable homotopy classes of mappings, and 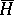 is reduced homology. The spectra
is reduced homology. The spectra  are the dual Brown–Gitler spectra. The Brown–Gitler spectra themselves can be obtained by the formula
are the dual Brown–Gitler spectra. The Brown–Gitler spectra themselves can be obtained by the formula
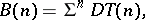 |
where  denotes the Spanier–Whitehead duality functor. The suspension factor is a normalization introduced to put the bottom cohomology class of
denotes the Spanier–Whitehead duality functor. The suspension factor is a normalization introduced to put the bottom cohomology class of  in degree
in degree  . An easy calculation shows that
. An easy calculation shows that  for all prime numbers and all
for all prime numbers and all  .
.
For a general spectrum  and
and  modulo
modulo  , the group
, the group 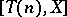 is naturally isomorphic to the group
is naturally isomorphic to the group 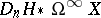 of homogeneous elements of degree
of homogeneous elements of degree  in the Cartier–Dieudonné module
in the Cartier–Dieudonné module 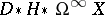 of the Abelian Hopf algebra
of the Abelian Hopf algebra  . In fact, one way to construct the Brown–Gitler spectra is to note that the functor
. In fact, one way to construct the Brown–Gitler spectra is to note that the functor
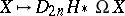 |
is the degree- group of an extraordinary homology theory; then
group of an extraordinary homology theory; then  is the
is the  -completion of the representing spectrum. See [a6]. This can be greatly, but not completely, destabilized. See [a7].
-completion of the representing spectrum. See [a6]. This can be greatly, but not completely, destabilized. See [a7].
References
| [a1] | E.H. Brown Jr., S. Gitler, "A spectrum whose cohomology is a certain cyclic module over the Steenrod algebra" Topology , 12 (1973) pp. 283–295 |
| [a2] | E.H. Brown Jr., F.P. Peterson, "A universal space for normal bundles of  -manifolds" Comment. Math. Helv. , 54 : 3 (1979) pp. 405–430 -manifolds" Comment. Math. Helv. , 54 : 3 (1979) pp. 405–430 |
| [a3] | G. Carlsson, "G.B. Segal's Burnside ring conjecture for 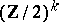 " Topology , 22 (1983) pp. 83–103 " Topology , 22 (1983) pp. 83–103 |
| [a4] | R.L. Cohen, "Odd primary infinite families in stable homotopy theory" Memoirs Amer. Math. Soc. , 30 : 242 (1981) |
| [a5] | R.L. Cohen, "The immersion conjecture for differentiable manifolds" Ann. of Math. (2) , 122 : 2 (1985) pp. 237–328 |
| [a6] | P. Goerss, J. Lannes, F. Morel, "Hopf algebras, Witt vectors, and Brown–Gitler spectra" , Algebraic Topology (Oaxtepec, 1991) , Contemp. Math. , 146 , Amer. Math. Soc. (1993) pp. 111–128 |
| [a7] | P. Goerss, J. Lannes, F. Morel, "Vecteurs de Witt non-commutatifs et représentabilité de l'homologie modulo 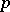 " Invent. Math. , 108 : 1 (1992) pp. 163–227 " Invent. Math. , 108 : 1 (1992) pp. 163–227 |
| [a8] | J. Lannes, "Sur les espaces fonctionnels dont la source est le classifiant d'un 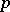 -groupe abélien élémentaire" IHES Publ. Math. , 75 (1992) pp. 135–244 -groupe abélien élémentaire" IHES Publ. Math. , 75 (1992) pp. 135–244 |
| [a9] | M. Mahowald, "A new infinite family in 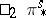 " Topology , 16 : 3 (1977) pp. 249–256 " Topology , 16 : 3 (1977) pp. 249–256 |
| [a10] | H. Miller, "The Sullivan conjecture on maps from classifying spaces" Ann. of Math. (2) , 120 : 1 (1984) pp. 39–87 |
Brown-Gitler spectra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brown-Gitler_spectra&oldid=17469