Branch-and-bound algorithm
Consider a (mixed) integer linear programming problem
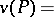 |
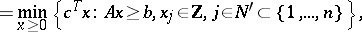 |
where 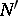 is the set of variables that are required to be integer,
is the set of variables that are required to be integer, 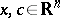 ,
, 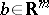 , and
, and 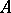 is an
is an 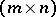 -matrix. For convenience and without loss of generality, assume that
-matrix. For convenience and without loss of generality, assume that 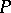 is bounded. Let
is bounded. Let 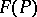 be the feasible set of
be the feasible set of 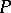 and
and 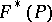 the set of optimal solutions, i.e.,
the set of optimal solutions, i.e.,
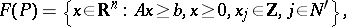 |
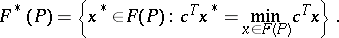 |
In branch-and-bound methods, the above problem is split up into a number of subproblems by partitioning the feasible set in some way. These subproblems are examined in turn and can be further split up. This is the branching part. Bounds on the optimal values of the subproblems are used to discard certain subproblems as irrelevant, or to perform a further decomposition.
In somewhat more detail, let 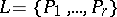 be the current list of subproblems,
be the current list of subproblems, 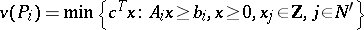 . Let
. Let 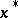 be the currently best point of
be the currently best point of 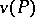 , the incumbent, and
, the incumbent, and 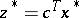 the currently best value, sometimes called the cutting value. The process is begun from
the currently best value, sometimes called the cutting value. The process is begun from  ,
, 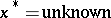 ,
, 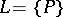 .
.
Now take a 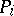 and consider its linear programming relaxation
and consider its linear programming relaxation 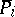 :
:
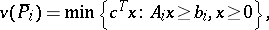 |
obtained by discarding the integrality constraint. Solve 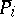 . If
. If 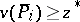 , no point of
, no point of 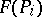 does better than any already obtained, and
does better than any already obtained, and 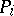 can be discarded. One says that in this case
can be discarded. One says that in this case 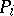 has been fathomed.
has been fathomed.
If 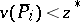 , there are two subcases:
, there are two subcases:
a) 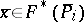 and
and 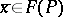 . Then
. Then 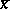 is optimal in
is optimal in 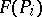 and
and 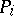 has also been fathomed. The new values of
has also been fathomed. The new values of 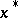 and
and 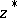 are
are 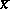 and
and 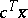 , and
, and 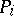 is discarded.
is discarded.
b) 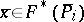 and
and 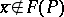 (i.e., an integrality constraint is violated). Then
(i.e., an integrality constraint is violated). Then 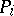 is split up into certain subproblems, which are added to the list
is split up into certain subproblems, which are added to the list 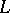 ,
, 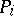 is removed and the incumbent and cutting value remain the same.
is removed and the incumbent and cutting value remain the same.
The algorithm ends when 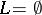 .
.
This description does not yet say anything about how to split up a 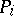 . One method often used is to pick a
. One method often used is to pick a 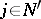 for which
for which  is not integral and to split up
is not integral and to split up 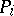 into the two subproblems defined by the respective constraints:
into the two subproblems defined by the respective constraints:
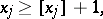 |
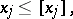 |
where 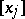 denotes the entier (or integral part) of
denotes the entier (or integral part) of 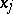 , the largest integer less than or equal to
, the largest integer less than or equal to 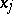 .
.
In the above, the linear programming relaxation 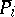 has been used to obtain bounds on
has been used to obtain bounds on 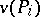 . This can be replaced with other ideas, e.g., Lagrangean relaxation.
. This can be replaced with other ideas, e.g., Lagrangean relaxation.
In [a5], there is a useful flow chart of branch and bound. The branch-and-bound idea was introduced in [a1] and improved in [a2]. Some standard references are [a3], [a4], [a5], [a6].
References
| [a1] | A.H. Land, A.G. Doig, "An automatic method for solving discrete programming problems" Econometrica , 28 (1960) pp. 497–520 |
| [a2] | R.J. Dakin, "A tree-search algorithm for mixed integer programming problems" Comp. J. , 8 (1965) pp. 250–255 |
| [a3] | C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization" , Prentice-Hall (1982) |
| [a4] | S. Walukiewicz, "Integer programming" , Kluwer Acad. Publ. (1991) |
| [a5] | S. Zionts, "Linear and integer programming" , Prentice-Hall (1974) |
| [a6] | G.L. Nemhauser, L.A. Wolsey, "Integer programming" G.L. Nemhauser (ed.) A.H.G. Rinnooy Kan (ed.) M.J. Todd (ed.) , Optimization , North-Holland (1989) pp. 447–528 |
Branch-and-bound algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branch-and-bound_algorithm&oldid=17467