Differential entropy
The formal analogue of the concept of entropy for random variables having distribution densities. The differential entropy  of a random variable
of a random variable  defined on some probability space
defined on some probability space  , assuming values in an
, assuming values in an  -dimensional Euclidean space
-dimensional Euclidean space  and having distribution density
and having distribution density  ,
,  , is given by the formula
, is given by the formula
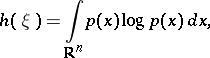 |
where  is assumed to be equal to zero. Thus, the differential entropy coincides with the entropy of the measure
is assumed to be equal to zero. Thus, the differential entropy coincides with the entropy of the measure 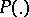 with respect to the Lebesgue measure
with respect to the Lebesgue measure 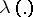 , where
, where 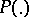 is the distribution of
is the distribution of 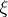 .
.
The concept of the differential entropy proves useful in computing various information-theoretic characteristics, in the first place the mutual amount of information (cf. Information, amount of) 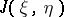 of two random vectors
of two random vectors 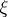 and
and 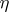 . If
. If  ,
, 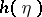 and
and 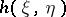 (i.e. the differential entropy of the pair
(i.e. the differential entropy of the pair 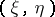 ) are finite, the following formula is valid:
) are finite, the following formula is valid:
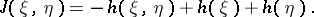 |
The following two properties of the differential entropy are worthy of mention: 1) as distinct from the ordinary entropy, the differential entropy is not covariant with respect to a change in the coordinate system and may assume negative values; and 2) let  be the discretization of an
be the discretization of an  -dimensional random variable
-dimensional random variable 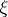 having a density, with steps of
having a density, with steps of 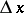 ; then for the entropy
; then for the entropy 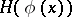 the formula
the formula
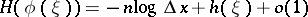 |
is valid as  . Thus,
. Thus, 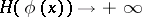 as
as  . The principal term of the asymptotics of
. The principal term of the asymptotics of 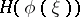 depends on the dimension of the space of values of
depends on the dimension of the space of values of 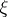 . The differential entropy defines the term next in order of the asymptotic expansion independent of
. The differential entropy defines the term next in order of the asymptotic expansion independent of  and it is the first term involving a dependence on the actual nature of the distribution of
and it is the first term involving a dependence on the actual nature of the distribution of 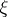 .
.
References
| [1] | I.M. Gel'fand, A.N. Kolmogorov, A.M. Yaglom, "The amount of information in, and entropy of, continuous distributions" , Proc. 3-rd All-Union Math. Congress , 3 , Moscow (1958) pp. 300–320 (In Russian) |
| [2] | A. Rényi, "Wahrscheinlichkeitsrechnung" , Deutsch. Verlag Wissenschaft. (1962) |
Differential entropy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_entropy&oldid=17439