Chebyshev constant
A numerical invariant  of a compact set
of a compact set  in the complex plane that is used in the theory of best approximation.
in the complex plane that is used in the theory of best approximation.
Let  be the class of all polynomials
be the class of all polynomials
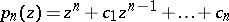 |
of degree  , and let
, and let
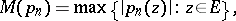 |
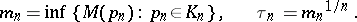 |
There exists a polynomial  for which
for which  ; it is called the Chebyshev polynomial for
; it is called the Chebyshev polynomial for 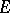 . Moreover, the limit
. Moreover, the limit
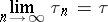 |
exists, and is called the Chebyshev constant for 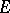 .
.
Restricting oneself to the class  of all polynomials
of all polynomials
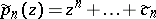 |
all zeros of which lie in 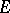 , one obtains corresponding values
, one obtains corresponding values 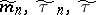 and a polynomial
and a polynomial  for which
for which  (it is also called the Chebyshev polynomial).
(it is also called the Chebyshev polynomial).
It is known that 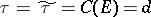 , where
, where 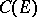 is the capacity of the compact set
is the capacity of the compact set  , and
, and 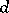 is its transfinite diameter (cf., for example, [1]).
is its transfinite diameter (cf., for example, [1]).
The concept of the Chebyshev constant generalizes to compact sets 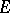 in higher-dimensional Euclidean spaces
in higher-dimensional Euclidean spaces  starting from potential theory. For a point
starting from potential theory. For a point 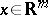 , let
, let
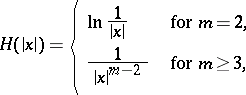 |
be the fundamental solution of the Laplace equation, and for a set  , let
, let
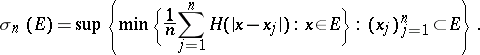 |
Then for  one obtains the relation
one obtains the relation
 |
and for 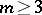 one obtains (cf. [2]):
one obtains (cf. [2]):
 |
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) |
Comments
References
| [a1] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
| [a2] | J.L. Walsh, "Interpolation and approximation by rational functions in the complex domain" , Amer. Math. Soc. (1956) |
Chebyshev constant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_constant&oldid=17435