Diffeomorphism
differentiable homeomorphism, smooth homeomorphism
A one-to-one continuously-differentiable mapping  of a differentiable manifold
of a differentiable manifold  (e.g. of a domain in a Euclidean space) into a differentiable manifold
(e.g. of a domain in a Euclidean space) into a differentiable manifold  for which the inverse mapping is also continuously differentiable. If
for which the inverse mapping is also continuously differentiable. If  , one says that
, one says that  and
and  are diffeomorphic. From the point of view of differential topology, diffeomorphic manifolds have the same properties, and one is interested in a classification of manifolds up to a diffeomorphism (this classification is not identical with the coarser classification up to a homeomorphism, except for cases involving small dimensions).
are diffeomorphic. From the point of view of differential topology, diffeomorphic manifolds have the same properties, and one is interested in a classification of manifolds up to a diffeomorphism (this classification is not identical with the coarser classification up to a homeomorphism, except for cases involving small dimensions).
Even though the term "diffeomorphism" was introduced comparatively recently, in practice numerous transformations and changes of variables which have been used in mathematics for long periods of time are diffeomorphisms, while many families of transformations are groups of diffeomorphisms. This applies, in particular, to diffeomorphisms which preserve a supplementary structure on the manifold (e.g. a contact, symplectic, conformal, or complex structure). In the past such diffeomorphisms had special appellations (in the above examples, contact transformations, canonical mappings, conformal mappings, and biholomorphic mappings), and these are often replaced at the time of writing (1970s) by the term "diffeomorphism" with an adjective characterizing the preserved structure (e.g. "symplectic diffeomorphismsymplectic diffeomorphism" rather than "canonical transformation" ).
Topological (more exactly, homotopic) properties of the group  of all diffeomorphisms of a manifold
of all diffeomorphisms of a manifold  onto itself, in which a topology has been introduced in a suitable manner, have also been studied. They may be unexpectedly complicated (see, e.g., [1], [4], [5], which also contain reviews and references). This problem is connected with a number of important problems in homotopic topology (e.g. with the homotopy groups of spheres). In principle, knowledge of the properties of
onto itself, in which a topology has been introduced in a suitable manner, have also been studied. They may be unexpectedly complicated (see, e.g., [1], [4], [5], which also contain reviews and references). This problem is connected with a number of important problems in homotopic topology (e.g. with the homotopy groups of spheres). In principle, knowledge of the properties of  would be of assistance in solving these problems, but at the time of writing (1987) the situation seems to be almost the opposite: Advances in the study of
would be of assistance in solving these problems, but at the time of writing (1987) the situation seems to be almost the opposite: Advances in the study of  involve the use of the already known features of the problems or, at best, are realized in parallel with the solutions of these problems and by the same methods. As regards the algebraic properties of the group of diffeomorphisms of class
involve the use of the already known features of the problems or, at best, are realized in parallel with the solutions of these problems and by the same methods. As regards the algebraic properties of the group of diffeomorphisms of class 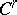 (including the case
(including the case 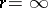 ) of a closed
) of a closed  -dimensional manifold, it has been proved that if
-dimensional manifold, it has been proved that if 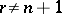 , then its connected component of the unit is a simple group, i.e. has no non-trivial normal subgroups (see Normal subgroup; cf. [2], ; the situation is not clear for
, then its connected component of the unit is a simple group, i.e. has no non-trivial normal subgroups (see Normal subgroup; cf. [2], ; the situation is not clear for 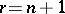 ). As regards a non-closed
). As regards a non-closed  -dimensional manifold
-dimensional manifold 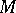 , it has been proved that the group of all diffeomorphisms of class
, it has been proved that the group of all diffeomorphisms of class 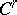 (
(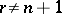 ) which may be connected with the identity mapping
) which may be connected with the identity mapping  by way of a continuous family of diffeomorphisms
by way of a continuous family of diffeomorphisms 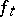 (
( ,
, 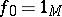 ;
; 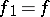 ) which does not displace points outside a certain compact set (depending on the family), is simple.
) which does not displace points outside a certain compact set (depending on the family), is simple.
References
| [1] | P.L. Antonelli, D. Burghelea, P.J. Kahn, "The non-finite homotopy type of some diffeomorphism groups" Topology , 11 : 1 (1972) pp. 1–49 |
| [2] | W. Thurston, "Foliations and groups of diffeomorphisms" Bull. Amer. Math. Soc. , 80 : 2 (1974) pp. 304–307 |
| [3a] | J.N. Mather, "Commutators of diffeomorphisms" Comm. Math. Helv. , 49 : 4 (1974) pp. 512–528 |
| [3b] | J.N. Mather, "Commutators of diffeomorphisms II" Comm. Math. Helv. , 50 : 1 (1975) pp. 33–40 |
| [4] | F.T. Farrell, W.C. Hsiang, "On the rational homotopy groups of the diffeomorphism groups of disks, spheres and aspherical manifolds" R.J. Milgram (ed.) , Algebraic and geometric topology , Proc. Symp. Pure Math. , 32.1 , Amer. Math. Soc. (1978) pp. 325–328 |
| [5] | D. Burghelea, R. Lashof, "Geometric transfer and the homotopy type of the automorphism groups of a manifold" Trans. Amer. Math. Soc. , 269 : 1 (1982) pp. 1–38 |
Comments
The diffeomorphism classification of compact two-dimensional manifolds is presented in [a1]. For manifolds of dimensions three or fewer the classification by diffeomorphism, homeomorphism and combinatorial equivalence coincide; see [a5], [a6]. For compact simply-connected manifolds 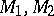 of dimension
of dimension 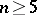 one of the most useful tools for obtaining a diffeomorphism is the
one of the most useful tools for obtaining a diffeomorphism is the 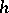 -cobordism theorem of Smale [a7], see also [a4]:
-cobordism theorem of Smale [a7], see also [a4]: 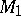 and
and 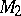 are diffeomorphic provided there is a compact manifold
are diffeomorphic provided there is a compact manifold 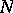 of dimension
of dimension  whose boundary is the disjoint union
whose boundary is the disjoint union 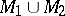 , and both
, and both 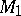 and
and 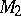 are deformation retracts of
are deformation retracts of 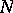 (cf. Deformation retract;
(cf. Deformation retract; 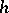 -cobordism). In fact, in this case
-cobordism). In fact, in this case 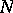 is diffeomorphic to the Cartesian product of
is diffeomorphic to the Cartesian product of 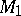 (or
(or 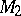 ) and the closed unit interval.
) and the closed unit interval.
Many further results have been obtained by combining the 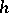 -cobordism theorem with other tools from algebraic and differential topology; see [a1], [a3].
-cobordism theorem with other tools from algebraic and differential topology; see [a1], [a3].
References
| [a1] | W.B. Browder, "Surgery on simply-connected manifolds" , Springer (1972) |
| [a2] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. Chapt. 6 |
| [a3] | R.C. Kirby, L.C. Siebenmann, "Foundational essays on topological manifolds, smoothings, and triangulations" , Princeton Univ. Press (1977) pp. 155–213 |
| [a4] | J. Milnor, "Lecture notes on the 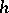 -cobordism theorem" , Princeton Univ. Press (1965) -cobordism theorem" , Princeton Univ. Press (1965) |
| [a5] | E.E. Moise, "Geometric topology in dimensions 2 and 3" , Springer (1977) |
| [a6] | J. Munkres, "Obstructions to smoothing of piecewise-differentiable homeomorphisms" Ann. of Math. , 72 (1960) pp. 521–554 |
| [a7] | S. Smale, "On the structure of manifolds" Amer. J. Math. , 84 (1962) pp. 387–399 |
Diffeomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diffeomorphism&oldid=17426