Hensel ring
A commutative local ring to which the Hensel lemma applies, or, according to another definition, to which the implicit function theorem applies. For a local ring  with maximal ideal
with maximal ideal  the former definition means that for any unitary polynomial
the former definition means that for any unitary polynomial  and a simple solution
and a simple solution  of the equation
of the equation  (
( ) (i.e.
) (i.e.  and
and  ) there exists an
) there exists an  such that
such that  and
and  (
( ).
).
Examples of Hensel rings include complete local rings, rings of convergent power series (and, in a general sense, analytic rings, cf. Analytic ring), and the ring of algebraic power series (i.e. series from  which are algebraic over
which are algebraic over 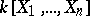 ). A local ring that is integral over a Hensel ring is a Hensel ring; in particular, a quotient ring of a Hensel ring is a Hensel ring. For any local ring
). A local ring that is integral over a Hensel ring is a Hensel ring; in particular, a quotient ring of a Hensel ring is a Hensel ring. For any local ring 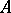 there exists a general construct — a local Hensel
there exists a general construct — a local Hensel  -algebra
-algebra 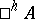 such that for any local Hensel
such that for any local Hensel  -algebra
-algebra  there exists a unique homomorphism of
there exists a unique homomorphism of  -algebras
-algebras 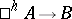 . The algebra
. The algebra  of a local ring
of a local ring  is a strictly-flat
is a strictly-flat 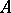 -module,
-module,  will be a maximal ideal of
will be a maximal ideal of  , the residue fields of
, the residue fields of  and
and  are canonically isomorphic, and the completions of
are canonically isomorphic, and the completions of  and
and  (in the topologies of the local rings) coincide. Thus, the ring of algebraic power series in
(in the topologies of the local rings) coincide. Thus, the ring of algebraic power series in  is a Hensel
is a Hensel  -algebra for
-algebra for  . If
. If  is a Noetherian (or, respectively, reduced, normal, regular, excellent) ring, so is
is a Noetherian (or, respectively, reduced, normal, regular, excellent) ring, so is  . Conversely, if
. Conversely, if  is an integral ring,
is an integral ring,  need not be integral; more exactly, there exists a bijective correspondence between the maximal ideals of the integral closure of
need not be integral; more exactly, there exists a bijective correspondence between the maximal ideals of the integral closure of  and the minimal prime ideals of
and the minimal prime ideals of  .
.
A Hensel ring with a separably-closed residue field is called strictly local (or strictly Henselian), owing to the locality of its spectrum in the étale topology of schemes; in a manner similar to the construction of the Hensel  -algebra
-algebra 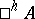 there is a strict Hensel
there is a strict Hensel  -algebra functor
-algebra functor 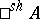 . The concept of a Hensel ring may be introduced for a semi-local ring and even, in a more-general sense, for the pair ring–ideal.
. The concept of a Hensel ring may be introduced for a semi-local ring and even, in a more-general sense, for the pair ring–ideal.
A Hensel ring may be described as a ring over which any finite algebra is a direct sum of local rings. Hensel rings were introduced in [1]; the general theory of Hensel rings and the construction of Hensel  -algebras are developed in [2].
-algebras are developed in [2].
In the theory of étale morphisms and étale topology a Hensel  -algebra is understood to be the inductive limit of étale extensions of the ring. In a commutative algebra a Hensel
-algebra is understood to be the inductive limit of étale extensions of the ring. In a commutative algebra a Hensel  -algebra often replaces the operation of completion, which plays an important role in local studies of objects.
-algebra often replaces the operation of completion, which plays an important role in local studies of objects.
References
| [1] | G. Azumaya, "On maximally central algebras" Nagoya Math. J. , 2 (1951) pp. 119–150 |
| [2] | M. Nagata, "Local rings" , Interscience (1962) |
| [3] | A. Grothendieck, "Eléments de géometrie algébrique. IV" Publ. Math. IHES : 32 (1967) |
Comments
The ring (algebra)  is called the Henselization or Hensel closure of the local ring
is called the Henselization or Hensel closure of the local ring  .
.
The ideal–ring pair formulation of the Hensel property is as follows. Let  be a pair consisting of a ring
be a pair consisting of a ring  and an ideal
and an ideal  . Then if
. Then if  is such that
is such that  and
and 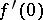 is a unit in
is a unit in 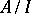 , then there exists an
, then there exists an  such that
such that  .
.
For a discussion of the solution of systems of polynomial equations and implicit-function type statements in the context of Hensel rings cf., for instance, [a2], Chapt. 2.
References
| [a1] | M. Raynaud, "Anneaux locaux Henséliens" , Lect. notes in math. , 169 , Springer (1970) |
| [a2] | H. Kurke, G. Pfister, M. Roczen, "Henselsche Ringe" , Deutsch. Verlag Wissenschaft. (1975) |
Hensel ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hensel_ring&oldid=17423