Quotient object
of an object in a category
A concept generalizing the notions of a quotient set, a quotient group, a quotient space, etc.
Let  be some class of epimorphisms in a category
be some class of epimorphisms in a category 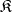 that contains all identity morphisms in
that contains all identity morphisms in 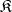 and is closed under multiplication on the right by isomorphisms. In other words, for every
and is closed under multiplication on the right by isomorphisms. In other words, for every 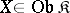 ,
, 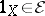 and for every
and for every  in
in 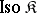 and every
and every  in
in 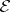 the morphism
the morphism 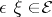 . Two morphisms
. Two morphisms  and
and 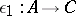 in
in 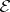 are said to be equivalent if
are said to be equivalent if 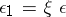 for some isomorphism
for some isomorphism  . The equivalence class of a morphism
. The equivalence class of a morphism  is called an
is called an 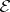 -quotient object of the object
-quotient object of the object 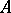 , and the pair
, and the pair 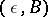 is called a representative of the quotient object. A quotient object with representative
is called a representative of the quotient object. A quotient object with representative 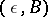 is sometimes denoted by
is sometimes denoted by 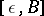 ,
, 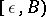 or simply by
or simply by 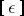 .
.
Every object 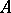 has at least one
has at least one 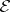 -quotient object, the improper quotient object
-quotient object, the improper quotient object  ; other quotient objects of
; other quotient objects of 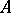 are called proper. A category
are called proper. A category  is called
is called 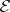 -locally small if for every object
-locally small if for every object 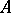 in
in 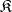 the class of
the class of 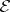 -quotient objects of
-quotient objects of 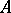 is a set.
is a set.
If one takes as 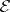 the subcategory of all epimorphisms,
the subcategory of all epimorphisms, 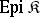 , then
, then 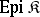 -quotient objects are simply called quotient objects. If
-quotient objects are simply called quotient objects. If 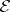 is part of a bicategory structure
is part of a bicategory structure 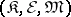 on
on 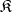 , then
, then 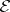 -quotient objects are called admissible quotient objects. Similarly, if
-quotient objects are called admissible quotient objects. Similarly, if 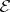 consists of all regular (strict, normal, etc.) epimorphisms, then the corresponding quotient objects are called regular (strict, normal, etc). For example, in the category of topological spaces quotient spaces correspond to regular quotient objects.
consists of all regular (strict, normal, etc.) epimorphisms, then the corresponding quotient objects are called regular (strict, normal, etc). For example, in the category of topological spaces quotient spaces correspond to regular quotient objects.
The concept of a quotient object of an object in a category is dual to that of a subobject.
Comments
The terms "colocally small categorycolocally small" and "co-well-powered categoryco-well-powered" are often used instead of "locally small" .
References
| [a1] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohoku Math. J. , 9 (1957) pp. 119–221 |
| [a2] | B. Mitchell, "Theory of categories" , Acad. Press (1965) pp. 7 |
Quotient object. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quotient_object&oldid=17419