Stein space
holomorphically-complete space
A paracompact complex analytic space 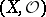 with the following properties:
with the following properties:
1) any compact analytic subset in 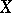 is finite (cf. Analytic set 6));
is finite (cf. Analytic set 6));
2) any compact set 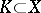 has an open neighbourhood
has an open neighbourhood 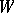 in
in 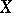 such that
such that
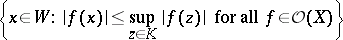 |
is compact (weak holomorphic convexity).
A complex manifold 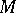 is a Stein space if and only if
is a Stein space if and only if 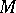 is a Stein manifold. A complex space is a Stein space if and only if its reduction has this property. Any holomorphically-convex open subspace in a Stein space is a Stein space. A reduced complex space is a Stein space if and only if its normalization is a Stein space. Any closed analytic subspace in a Stein space, for instance in
is a Stein manifold. A complex space is a Stein space if and only if its reduction has this property. Any holomorphically-convex open subspace in a Stein space is a Stein space. A reduced complex space is a Stein space if and only if its normalization is a Stein space. Any closed analytic subspace in a Stein space, for instance in 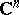 , is a Stein space. Any finite-dimensional Stein space has a proper injective holomorphic mapping (cf. Proper morphism) into some
, is a Stein space. Any finite-dimensional Stein space has a proper injective holomorphic mapping (cf. Proper morphism) into some 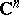 which is regular at every non-singular point. Any unramified covering of a Stein space is a Stein space. The direct product of two Stein spaces is a Stein space. In many cases a holomorphic fibre space whose base and fibres are Stein spaces is a Stein space (e.g. if the structure group is a complex Lie group with a finite number of connected components). However, there are holomorphic fibre spaces with fibre
which is regular at every non-singular point. Any unramified covering of a Stein space is a Stein space. The direct product of two Stein spaces is a Stein space. In many cases a holomorphic fibre space whose base and fibres are Stein spaces is a Stein space (e.g. if the structure group is a complex Lie group with a finite number of connected components). However, there are holomorphic fibre spaces with fibre 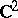 and base
and base 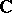 that are not Stein manifolds [2].
that are not Stein manifolds [2].
Let 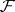 be a coherent analytic sheaf on a Stein space
be a coherent analytic sheaf on a Stein space 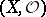 . Then the following theorems
. Then the following theorems 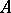 and
and 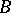 of H. Cartan (cf. Cartan theorem) hold:
of H. Cartan (cf. Cartan theorem) hold:
A) The space 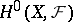 generates the stalk
generates the stalk 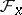 of the sheaf
of the sheaf 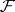 at any point
at any point 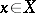 ;
;
B) 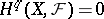 for all
for all 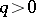 .
.
Conversely, if 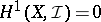 for any coherent sheaf of ideals
for any coherent sheaf of ideals 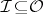 , then
, then 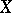 is a Stein space. A domain
is a Stein space. A domain 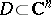 is a Stein manifold if and only if
is a Stein manifold if and only if 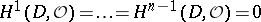 .
.
From the Cartan theorems it follows that on a Stein space the first Cousin problem is always solvable, and if 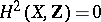 , then the second Cousin problem is solvable as well (see Cousin problems). On any Stein manifold
, then the second Cousin problem is solvable as well (see Cousin problems). On any Stein manifold 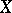 the Poincaré problem, i.e. can any meromorphic function be represented in the form
the Poincaré problem, i.e. can any meromorphic function be represented in the form 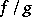 , where
, where 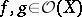 ,
, 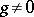 , is solvable. Furthermore, if
, is solvable. Furthermore, if 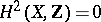 , then
, then 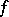 and
and 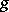 can be chosen in such a way that the germs
can be chosen in such a way that the germs 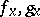 at any point
at any point 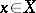 are relatively prime. The group of divisor classes of an irreducible reduced Stein space
are relatively prime. The group of divisor classes of an irreducible reduced Stein space  is isomorphic to
is isomorphic to 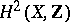 . For any
. For any  -dimensional Stein space
-dimensional Stein space 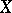 , the homology groups
, the homology groups 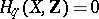 for
for 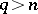 , and the group
, and the group 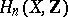 is torsion-free. If
is torsion-free. If 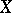 is a manifold, then
is a manifold, then 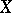 is homotopy equivalent to an
is homotopy equivalent to an  -dimensional cell complex. On the other hand, for any countable Abelian group
-dimensional cell complex. On the other hand, for any countable Abelian group  and any
and any 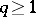 there is a domain of holomorphy
there is a domain of holomorphy 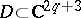 such that
such that 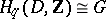 .
.
An important trend in the theory of Stein spaces is connected with studies of the plurisubharmonic functions on them (see Levi problem; Pseudo-convex and pseudo-concave). The basic result here is that a Stein space is characterized as a space on which there exists a strongly 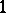 -pseudoconvex function exhausting it.
-pseudoconvex function exhausting it.
Algebras of holomorphic functions 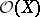 on a Stein space
on a Stein space 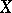 (so-called Stein algebras) have the following properties. For a maximal ideal
(so-called Stein algebras) have the following properties. For a maximal ideal 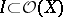 the following conditions are equivalent:
the following conditions are equivalent: 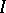 is closed in
is closed in 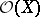 with respect to the topology of compact convergence;
with respect to the topology of compact convergence; 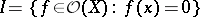 for some point
for some point 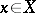 ; and
; and 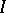 is finitely generated. If
is finitely generated. If 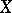 is finite-dimensional, then each character
is finite-dimensional, then each character 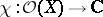 is of the form
is of the form 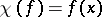 for some
for some 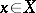 . If
. If 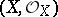 ,
, 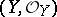 are two finite-dimensional Stein spaces with isomorphic algebras
are two finite-dimensional Stein spaces with isomorphic algebras 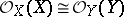 , then
, then 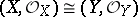 ; moreover, any isomorphism
; moreover, any isomorphism  is continuous and is induced by some isomorphism
is continuous and is induced by some isomorphism 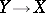 of complex spaces.
of complex spaces.
A significant role in the theory of Stein spaces is played by the so-called Oka principle, which states that a problem in the class of analytic functions on a Stein space is solvable if and only if it is solvable in the class of continuous functions. The second Cousin problem satisfies this principle. The following statement is still more general: The classification of the principal analytic fibrations (cf. Principal analytic fibration) with as basis a given reduced Stein space 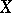 and as structure group a given complex Lie group
and as structure group a given complex Lie group 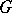 , coincides with the classification of the topological fibrations with the same basis and the same structure group. The groups of connected components in the groups of analytic and continuous functions
, coincides with the classification of the topological fibrations with the same basis and the same structure group. The groups of connected components in the groups of analytic and continuous functions 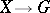 also coincide.
also coincide.
References
| [1] | H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1977) (Translated from German) |
| [2] | J.-P. Demailly, "Un example de fibré holomorphe non de Stein à fibre 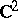 ayant pour base le disque ou le plan" Invent. Math. , 48 : 3 (1978) pp. 293–302 ayant pour base le disque ou le plan" Invent. Math. , 48 : 3 (1978) pp. 293–302 |
| [3a] | A.L. Onishchik, "Stein spaces" J. Soviet Math. , 4 : 5 (1974) pp. 540–554 Itogi Nauk. i Tekhn. Algebra.Topol. Geom. , 11 (1974) pp. 125–151 |
| [3b] | A.L. Onishchik, "Pseudoconvexity in the theory of complex spaces" J. Soviet Math. , 14 : 4 (1977) pp. 1363–1407 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 15 (1977) pp. 93–171 |
Comments
Let 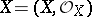 be a complex space. Let
be a complex space. Let 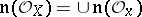 be the so-called nil radical of
be the so-called nil radical of 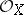 , i.e. the union of the nil radicals of the stalks
, i.e. the union of the nil radicals of the stalks 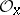 . It is a coherent sheaf (of ideals). The space
. It is a coherent sheaf (of ideals). The space 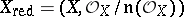 is called the reduction of
is called the reduction of 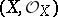 , as is the associated mapping
, as is the associated mapping 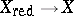 . A complex space
. A complex space 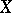 is called reduced at a point
is called reduced at a point 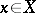 if
if 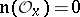 . The space
. The space 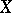 is called reduced if it is reduced at all its points (i.e. if
is called reduced if it is reduced at all its points (i.e. if 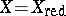 ).
).
The set 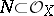 of elements not dividing zero is multiplicative (i.e.
of elements not dividing zero is multiplicative (i.e.  is open in
is open in 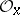 ;
; 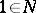 ; and
; and 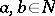 implies
implies 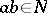 ). Hence
). Hence 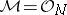 (with
(with 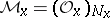 ,
, 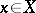 ) is a well-defined
) is a well-defined 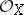 -module.
-module. 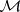 is called the sheaf of germs of meromorphic functions on
is called the sheaf of germs of meromorphic functions on 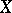 . The complex space
. The complex space 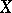 is called normal at
is called normal at 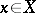 if
if 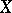 is reduced at
is reduced at  and
and 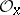 is integrally closed in
is integrally closed in 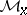 . A complex space is called normal if it is normal at every point. The normalization theorem says that for each reduced complex space
. A complex space is called normal if it is normal at every point. The normalization theorem says that for each reduced complex space 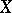 there are a normal complex space
there are a normal complex space 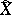 and a finite surjective holomorphic mapping
and a finite surjective holomorphic mapping 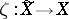 . The pair
. The pair 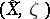 is called the normalization of
is called the normalization of 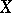 . It is uniquely defined up to analytic isomorphisms.
. It is uniquely defined up to analytic isomorphisms.
Finally, 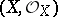 is called irreducible at
is called irreducible at  if
if 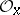 is an integral domain, and irreducible if it is irreducible at all points. See [1].
is an integral domain, and irreducible if it is irreducible at all points. See [1].
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) |
| [a2] | L. Kaup, B. Kaup, "Holomorphic functions of several variables" , de Gruyter (1983) (Translated from German) |
| [a3] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) pp. Chapt. 1, Sect. C |
Stein space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stein_space&oldid=17413