Universal property
A property of an object in a category which characterizes it as a representing object for some (covariant or contravariant) set-valued functor defined on the category. More formally, let 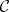 be a category and
be a category and 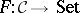 a functor (for definiteness, the covariant case is treated here). Then a universal element of
a functor (for definiteness, the covariant case is treated here). Then a universal element of 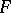 is a pair
is a pair 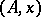 , where
, where 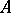 is an object of
is an object of 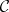 and
and 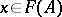 , such that for every other such pair
, such that for every other such pair 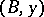 there is a unique
there is a unique 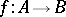 in
in  satisfying
satisfying 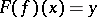 . The correspondence between
. The correspondence between 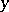 and
and 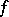 defines a natural isomorphism between
defines a natural isomorphism between 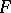 and the functor
and the functor 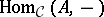 ; the object
; the object 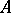 is said to be a representing object (or representation) for the functor
is said to be a representing object (or representation) for the functor 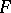 , and its universal property is the possession of the universal element
, and its universal property is the possession of the universal element  .
.
Examples.
1) In any category 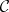 , the universal property of a (categorical) product
, the universal property of a (categorical) product 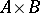 is the possession of a pair of projections
is the possession of a pair of projections 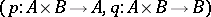 ; that is,
; that is, 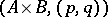 is a universal element for the (contravariant) functor which sends an object
is a universal element for the (contravariant) functor which sends an object 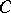 to the set of all pairs of morphisms
to the set of all pairs of morphisms 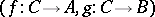 .
.
2) In the category of modules over a commutative ring 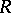 , the universal property of a tensor product
, the universal property of a tensor product 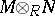 is the possession of a bilinear mapping
is the possession of a bilinear mapping 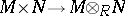 ; that is,
; that is, 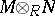 is a representing object for the covariant functor which sends a module
is a representing object for the covariant functor which sends a module 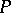 to the set of bilinear mappings
to the set of bilinear mappings  .
.
An object possessing a given universal property is unique up to canonical isomorphism in the appropriate category. The idea of characterizing objects by means of universal properties was first exploited by S. MacLane [a1].
References
| [a1] | S. MacLane, "Duality for groups" Bull. Amer. Math. Soc. , 56 (1950) pp. 485–516 |
Universal property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Universal_property&oldid=17411