Elementary divisors
of a matrix  over a polynomial ring
over a polynomial ring 
Powers of the monic irreducible polynomials over the field 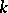 into which the invariant factors of
into which the invariant factors of 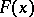 split. Two
split. Two 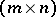 -matrices over
-matrices over 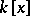 having the same rank are equivalent (that is, can be obtained from one another by means of elementary operations) if and only if they have the same system of elementary divisors.
having the same rank are equivalent (that is, can be obtained from one another by means of elementary operations) if and only if they have the same system of elementary divisors.
The elementary divisors of an  -matrix
-matrix  over
over  are, by definition, those of its characteristic matrix
are, by definition, those of its characteristic matrix 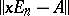 . They can be obtained in the following manner. Let
. They can be obtained in the following manner. Let 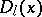 be the greatest common divisor of the minors of order
be the greatest common divisor of the minors of order 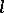 of the matrix
of the matrix 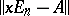 ,
, 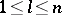 , and let
, and let 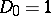 . Then the invariant factors of
. Then the invariant factors of 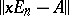 are
are
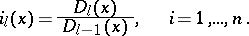 |
The factors 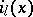 different from
different from 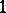 are in
are in 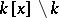 . Each of them can be represented in the form
. Each of them can be represented in the form
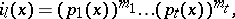 |
where the 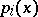 are monic irreducible polynomials over
are monic irreducible polynomials over 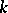 ,
, 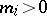 , and
, and 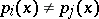 when
when 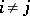 . All the polynomials
. All the polynomials 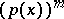 thus obtained form the system of elementary divisors of
thus obtained form the system of elementary divisors of 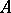 . Two square matrices over a field are similar if and only if they have the same system of elementary divisors. The product of all elementary divisors of a matrix over a field is its characteristic polynomial, and their least common multiple is its minimum polynomial. Any collection of polynomials of the form
. Two square matrices over a field are similar if and only if they have the same system of elementary divisors. The product of all elementary divisors of a matrix over a field is its characteristic polynomial, and their least common multiple is its minimum polynomial. Any collection of polynomials of the form  , where
, where 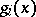 is a monic irreducible polynomial over
is a monic irreducible polynomial over 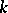 , is the system of elementary divisors for one and only one class of similar matrices over
, is the system of elementary divisors for one and only one class of similar matrices over 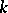 of order
of order  , where
, where  is the degree of the product of the
is the degree of the product of the 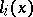 .
.
If 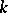 is a splitting field of the characteristic polynomial of
is a splitting field of the characteristic polynomial of 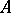 , then the elementary divisors have the form
, then the elementary divisors have the form 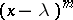 . Their number is then the same as the number of Jordan cells in the Jordan form of
. Their number is then the same as the number of Jordan cells in the Jordan form of 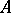 , and the elementary divisor
, and the elementary divisor 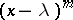 corresponds to a Jordan cell
corresponds to a Jordan cell 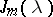 of order
of order  (see Jordan matrix). A square matrix over a field
(see Jordan matrix). A square matrix over a field 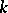 is similar to a diagonal matrix if and only if each elementary divisor of it has the form
is similar to a diagonal matrix if and only if each elementary divisor of it has the form 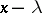 , where
, where 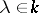 .
.
Comments
References
| [a1] | N. Jacobson, "Lectures in abstract algebra" , II. Linear algebra , v. Nostrand (1953) |
| [a2] | N. Jacobson, "Basic algebra" , I , Freeman (1974) |
Elementary divisors. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_divisors&oldid=17374