Jacobi matrix
From Encyclopedia of Mathematics
A square matrix 
with real entries such that 
for 
. If one writes 
(
), 
, and 
(
), then a Jacobi matrix has the form
 |
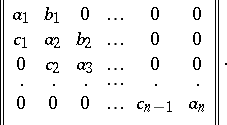Any minor of a Jacobi matrix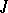 
is the product of certain principal minors of 
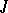and certain elements of 
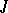. A Jacobi matrix 
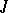is completely non-negative (that is, all its minors are non-negative) if and only if all its principal minors and all elements 
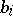and 
(
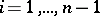) are non-negative. If 
for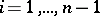 
, then the roots of the characteristic polynomial of 
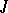are real and distinct.
References
| [1] | F.R. Gantmakher, M.G. Krein, "Oscillation matrices and kernels and small vibrations of mechanical systems" , Dept. Commerce USA. Joint Publ. Service (1961) (Translated from Russian) |
How to Cite This Entry:
Jacobi matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobi_matrix&oldid=17361
Jacobi matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobi_matrix&oldid=17361
This article was adapted from an original article by D.A. Suprunenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article