Eta-invariant

-invariant

Let be an unbounded self-adjoint operator with only pure point spectrum (cf. also Spectrum of an operator). Let be the eigenvalues of , counted with multiplicity. If is a first-order elliptic differential operator on a compact manifold, then and the series

is convergent for large enough. Moreover, 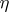has a meromorphic continuation to the complex plane, with a regular value (cf. also Analytic continuation). The value of at is called the eta-invariant of 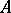, and was introduced by M.F. Atiyah, V.K. Patodi and I.M. Singer in the foundational paper [a1] as a correction term for an index theorem on manifolds with boundary (cf. also Index formulas). For example, in that paper, they prove that the signature 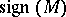of a compact, oriented, 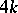-dimensional Riemannian manifold with boundary 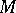whose metric is a product metric near the boundary is

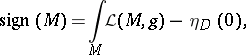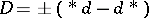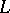where is the signature operator on the boundary and the Hirzebruch -polynomial associated to the Riemannian metric on .

The definition of the eta-invariant was generalized by J.-M. Bismut and J. Cheeger in [a2], where they introduced the eta-form of a family of elliptic operators as above. It can be used to recover the eta-invariant of operators in the family.

References

[a1]	M.F. Atiyah, V.K. Patodi, I.M. Singer, "Spectral asymmetry and Riemannian Geometry" Math. Proc. Cambridge Philos. Soc. , 77 (1975) pp. 43–69
[a2]	J.-M. Bismut, J. Cheeger, "Eta invariants and their adiabatic limits" J. Amer. Math. Soc. , 2 : 1 (1989) pp. 33–77