Union of sets

sum of sets

One of the basic operations on (collections of) sets. Suppose one has some (finite or infinite) collection 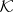of sets. Then the collection of all elements that belong to at least one of the sets in is called the union, or, more rarely, the sum, of (the sets in) ; it is denoted by .

Comments

In case , the union is also denoted by , , , or, more rarely, by .

In the Zermelo–Fraenkel axiom system for set theory, the sum-set axiom expresses that the union of a set of sets is a set.

If the sets 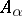are disjoint, then in the category the union of the objects 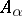is the sum of these objects in the categorical sense. In general, the sum of objects 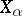is the disjoint union 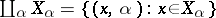. The natural imbeddings are given by . Thus, 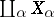together with the 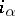, , 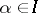satisfies the universal property for categorical sums: For every family of mappings 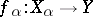there is a unique mapping such that .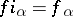

References

[a1]	K. Kuratowski, "Introduction to set theory and topology" , Pergamon (1961) pp. 25 (Translated from French)