Lefschetz number

An invariant of a mapping of a chain (cochain) complex or topological space into itself. Let be a chain complex of Abelian groups (respectively, a topological space), an endomorphism of degree 0 (respectively, a continuous mapping; cf. Degree of a mapping), the homology group of the object with coefficients in the field of rational numbers , where

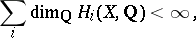and let be the trace of the linear transformation

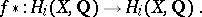By definition, the Lefschetz number of is

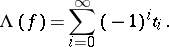In the case of a cochain complex the definition is similar. In particular, the Lefschetz number of the identity mapping is equal to the Euler characteristic of the object . If is a chain (cochain) complex of free Abelian groups or a topological space, then the number 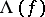is always an integer. The Lefschetz number was introduced by S. Lefschetz [1] for the solution of the problem on the number of fixed points of a continuous mapping (see Lefschetz formula).

To find the Lefschetz number of an endomorphism of a complex 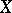consisting of finite-dimensional vector spaces over one can use the following formula (which is sometimes called the Hopf trace formula):

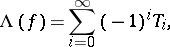where is the trace of the linear transformation 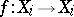. In particular, if 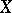is a finite cellular space, is a continuous mapping of it into itself and is a cellular approximation of 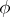, then

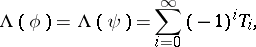where is the trace of the transformation

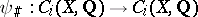induced by and 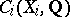is the group of rational 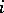-dimensional chains of .

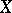Everything stated above can be generalized to the case of an arbitrary coefficient field.

References

[1]	S. Lefschetz, "Intersections and transformations of complexes and manifolds" Trans. Amer. Math. Soc. , 28 (1926) pp. 1–49
[2]	H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German)

References

[a1]	J. Dugundji, A. Granas, "Fixed point theory" , PWN (1982)