Vector space

linear space, over a field

An Abelian group 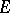, written additively, in which a multiplication of the elements by scalars is defined, i.e. a mapping

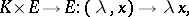which satisfies the following axioms (; ):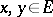

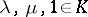1) ;

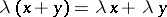2) ;

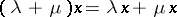3) ;

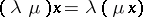4) .

Axioms 1)–4) imply the following important properties of a vector space ():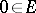

5) ;

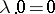6) ;

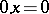7) .

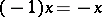The elements of the vector space are called its points, or vectors; the elements of 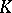are called scalars.

The vector spaces most often employed in mathematics and in its applications are those over the field 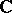of complex numbers and over the field 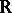of real numbers; they are said to be complex, respectively real, vector spaces.

The axioms of vector spaces express algebraic properties of many classes of objects which are frequently encountered in analysis. The most fundamental and the earliest examples of vector spaces are the -dimensional Euclidean spaces. Of almost equal importance are many function spaces: spaces of continuous functions, spaces of measurable functions, spaces of summable functions, spaces of analytic functions, and spaces of functions of bounded variation.

The concept of a vector space is a special case of the concept of a module over a ring — a vector space is a unitary module over a field. A unitary module over a non-commutative skew-field is also called a vector space over a skew-field; the theory of such vector spaces is much more difficult than the theory of vector spaces over a field.

One important task connected with vector spaces is the study of the geometry of vector spaces, i.e. the study of lines in vector spaces, flat and convex sets in vector spaces, vector subspaces, and bases in vector spaces.

A vector subspace, or simply a subspace, of a vector space 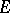is a subset 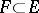that is closed with respect to the operations of addition and multiplication by a scalar. A subspace, considered apart from its ambient space, is a vector space over the ground field.

The straight line passing through two points and 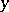of a vector space 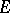is the set of elements 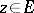of the form 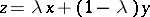, 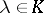. A set 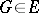is said to be a flat set if, in addition to two arbitrary points, it also contains the straight line passing through these points. Any flat set is obtained from some subspace by a parallel shift: 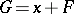; this means that each element 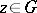can be uniquely represented in the form 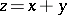, , 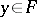and that this equation realizes a one-to-one correspondence between 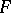and .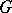

The totality of all shifts 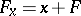of a given subspace 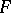forms a vector space over 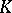, called the quotient space 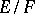, if the operations are defined as follows:

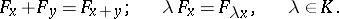Let 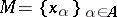be an arbitrary set of vectors in 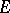. A linear combination of the vectors is a vector defined by an expression

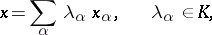in which only a finite number of coefficients differ from zero. The set of all linear combinations of vectors of the set 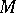is the smallest subspace containing 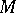and is said to be the linear envelope of the set 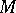. A linear combination is said to be trivial if all coefficients 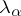are zero. The set 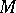is said to be a linearly independent set if all non-trivial linear combinations of vectors in 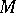are non-zero.

Any linearly independent set is contained in some maximal linearly independent set 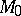, i.e. in a set which ceases to be linearly independent after any element in 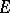has been added to it.

Each element 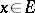may be uniquely represented as a linear combination of elements of a maximal linearly independent set:

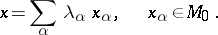A maximal linearly independent set is said to be a basis (an algebraic basis) of the vector space for this reason. All bases of a given vector space have the same cardinality, which is known as the dimension of the vector space. If this cardinality is finite, the space is said to be finite-dimensional; otherwise it is known as an infinite-dimensional vector space.

The field 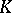may be considered as a one-dimensional vector space over itself; a basis of this vector space is a single element, which may be any element other than zero. A finite-dimensional vector space with a basis of elements is known as an -dimensional space.

The theory of convex sets plays an important part in the theory of real and complex vector spaces (cf. also Convex set). A set 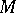in a real vector space is said to be a convex set if for any two points 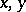in it the segment 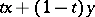, , 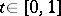also belongs to .

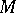The theory of linear functionals on vector spaces and the related theory of duality are important parts of the theory of vector spaces. Let 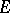be a vector space over a field 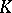. An additive and homogeneous mapping 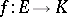, i.e.

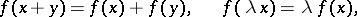is said to be a linear functional on 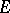. The set 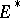of all linear functionals on 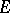forms a vector space over 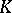with respect to the operations

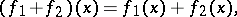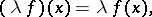This vector space is said to be the conjugate, or dual, space of 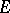. Several geometrical notions are connected with the concept of a conjugate space. Let 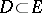(respectively, 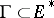); the set

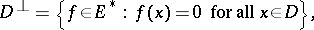or 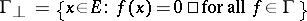, is said to be the annihilator or orthogonal complement of 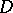(respectively, of 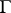); here 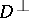and 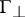are subspaces of 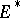and 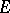, respectively. If 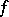is a non-zero element of 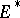, 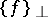is a maximal proper linear subspace in 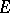, which is sometimes called a hypersubspace; a shift of such a subspace is said to be a hyperplane in 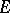; thus, any hyperplane has the form

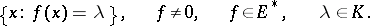If 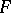is a subspace of the vector space 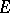, there exist natural isomorphisms between 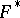and 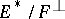and between 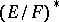and .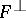

A subset is said to be a total subset over 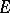if its annihilator contains only the zero element, .

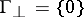Each linearly independent set 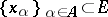can be brought into correspondence with a conjugate set 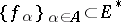, i.e. with a set such that 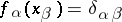(the Kronecker symbol) for all 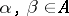. The set of pairs 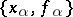is said to be a biorthogonal system. If the set 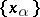is a basis in 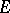, then 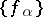is total over .

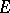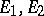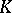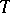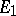An important chapter in the theory of vector spaces is the theory of linear transformations of these spaces. Let be two vector spaces over the same field . Then an additive and homogeneous mapping of into 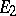, i.e.

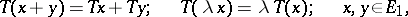is said to be a linear mapping or linear operator, mapping 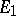into 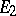(or from 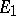into 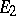). A special case of this concept is a linear functional, or a linear operator from 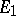into 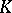. An example of a linear mapping is the natural mapping from 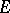into the quotient space 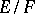, which establishes a one-to-one correspondence between each element 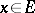and the flat set 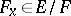. The set 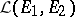of all linear operators 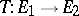forms a vector space with respect to the operations

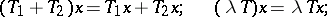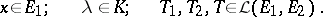Two vector spaces 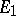and 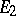are said to be isomorphic if there exists a linear operator (an "isomorphism" ) which realizes a one-to-one correspondence between their elements. 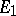and 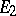are isomorphic if and only if their bases have equal cardinalities.

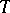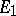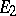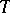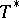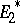Let be a linear operator from into . The conjugate linear operator, or dual linear operator, of is the linear operator from into 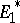defined by the equation

The relations 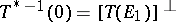, 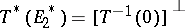are valid, which imply that 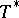is an isomorphism if and only if 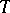is an isomorphism.

The theory of bilinear and multilinear mappings of vector spaces is closely connected with the theory of linear mappings of vector spaces (cf. Bilinear mapping; Multilinear mapping).

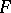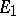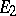Problems of extending linear mappings are an important group of problems in the theory of vector spaces. Let be a subspace of a vector space , let be a linear space over the same field as 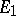and let 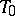be a linear mapping from 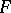into 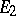; it is required to find an extension 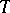of 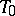which is defined on all of 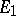and which is a linear mapping from 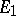into 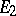. Such an extension always exists, but the problem may prove to be unsolvable owing to additional limitations imposed on the functions (which are related to supplementary structures in the vector space, e.g. to the topology or to an order relation). Examples of solutions of extension problems are the Hahn–Banach theorem and theorems on the extension of positive functionals in spaces with a cone.

An important branch of the theory of vector spaces is the theory of operations over a vector space, i.e. methods for constructing new vector spaces from given vector spaces. Examples of such operations are the well-known methods of taking a subspace and forming the quotient space by it. Other important operations include the construction of direct sums, direct products and tensor products of vector spaces.

Let 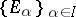be a family of vector spaces over a field 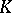. The set 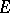which is the product of 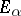can be made into a vector space over 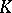by introducing the operations

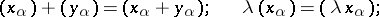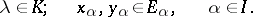The resulting vector space 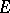is called the direct product of the vector spaces 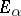, and is written as 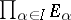. The subspace of the vector space 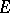consisting of all sequences for each of which the set 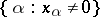is finite, is said to be the direct sum of the vector spaces 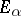, and is written as 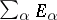or 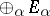. These two notions coincide if the number of terms is finite. In this case one uses the notations:

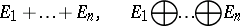or

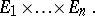Let 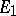and be vector spaces over the same field 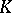; let 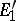, be total subspaces of the vector spaces , , 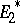and let be the vector space with the set of all elements of the space 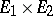as its basis. Each element 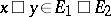can be brought into correspondence with a bilinear functi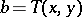on on 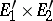using the formula 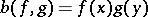, , 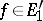. This mapping on the basis vectors 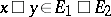may be extended to a linear mapping 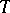from the vector space into the vector space of all bilinear functionals on 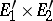. Let 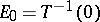. The tensor product of 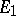and 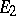is the quotient space 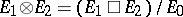; the image of the element is written as . 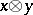The vector space 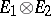is isomorphic to the vector space of bilinear functionals on 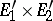(cf. Tensor product of vector spaces).

The most interesting part of the theory of vector spaces is the theory of finite-dimensional vector spaces. However, the concept of infinite-dimensional vector spaces has also proved fruitful and has interesting applications, especially in the theory of topological vector spaces, i.e. vector spaces equipped with topologies fitted in some manner to its algebraic structure.

References

[1]	N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French)
[2]	D.A. Raikov, "Vector spaces" , Noordhoff (1965) (Translated from Russian)
[3]	M.M. Day, "Normed linear spaces" , Springer (1958)
[4]	R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965)
[5]	P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958)
[6]	I.M. Glazman, Yu.I. Lyubich, "Finite-dimensional linear analysis: a systematic presentation in problem form" , M.I.T. (1974) (Translated from Russian)

References

[a1]	G. Strang, "Linear algebra and its applications" , Harcourt, Brace, Jovanovich (1988)
[a2]	B. Noble, J.W. Daniel, "Applied linear algebra" , Prentice-Hall (1977)
[a3]	W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. Sect. 2.7