Elliptic surface

An algebraic or analytic complete non-singular surface 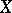having a fibration of elliptic curves (cf. Elliptic curve), that is, a morphism 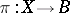onto a non-singular curve 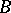whose generic fibre is a non-singular elliptic curve. Every elliptic surface is birationally (bimeromorphically) equivalent over 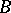to a unique minimal model, which is characterized by the fact that the fibre of does not contain exceptional curves of arithmetic genus 1. In what follows an elliptic surface is assumed to be minimal. Minimal elliptic surfaces have a more complicated structure than ruled surfaces. They can have singular fibres (that is, fibres that are not non-singular elliptic curves). There is a classification

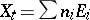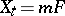of the singular fibres of elliptic surfaces. A singular fibre is called multiple if the greatest common divisor of the is , and then and 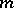is called the multiplicity of the fibre .

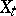On a minimal elliptic surface the canonical class 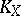contains a divisor that is a rational combination of fibres, in particular, 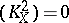. Moreover, the following formula holds for the canonical class (see [1], ):

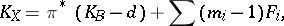where 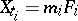are all the multiple fibres of 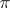and 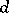is a divisor on of degree 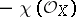. The topological Euler characteristic satisfies the formula

The classification of elliptic fibrations.

A fibration can be regarded as an elliptic curve over the function field . This curve, generally speaking, does not have the structure of an Abelian variety over . For this to happen it is necessary that it has a rational point over (and then is birationally isomorphic to the surface defined in 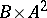by the Weierstrass equation 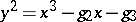, where 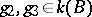). The specification of a rational point is equivalent to that of a section 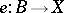such that ; a necessary condition for the existence of a section is the absence of multiple fibres. Fibrations without multiple fibres are called reduced. Every fibration, after a suitable ramified covering of the base, has a section (that is, is reduced) . Every fibration can also be made reduced by a sequence of transformations inverse to logarithmic ones

— local surgery of the fibration in neighbourhoods of fibres.

Reduced elliptic fibrations may be described as follows. To every such fibration 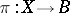corresponds a unique fibration 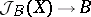that is a group object and is such that 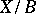is a principal homogeneous space over ; is the Jacobi fibration for 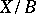; it characterizes the existence of a section. For a given Jacobi fibration 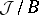, the set 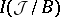of isomorphism classes of fibrations 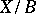for which has a cohomology description analogous to that of invertible sheaves (cf. Invertible sheaf). Here the role of 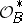is played by the sheaf of local sections . There is a natural one-to-one correspondence

under which the Jacobi fibration corresponds to the zero element. By means of one can distinguish between algebraic and non-algebraic fibrations: For a reduced fibration the surface is algebraic if and only if the element corresponding to it in is of finite order. The analogy with invertible sheaves can be pursued further. The analogue of the exact sequence

is the exact sequence

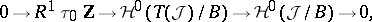where is the sheaf of local sections of the bundle and 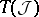is the tangent space to the fibre at . The boundary homomorphism

allows one to recognize when one fibration is a deformation of another. For that it is necessary and sufficient that the elements corresponding to these fibrations have one and the same image under (see ).

The classification of algebraic elliptic surfaces.

Suppose that . For an elliptic surface 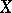the canonical dimension 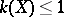, that is, it is equal to 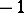, 0 or . If 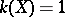, is said to be an elliptic surface of general type. These are characterized by the conditions and . Elliptic surfaces with or, more generally, with for some , are of general type.

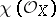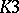Elliptic surfaces with are characterized by the condition . In this case can take the three values 2, 1 or . If , then is an elliptic -surface (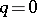, ). In this case is isomorphic to the projective line 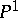, the fibration has no multiple fibres and has the invariants , , . If , then is an Enriques surface, that is, a surface with 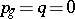, . (Every Enriques surface is elliptic.) In this case 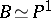, the fibration has two fibres of multiplicity 2, and has the invariants , . If , then two cases are possible. Either is an Abelian variety (and then , , ); or is a hyper-elliptic surface, that is, a surface that has a finite unramified covering — the product of two elliptic curves. 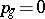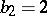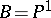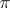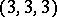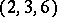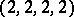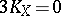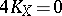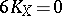In that case , , , , and has 3 or 4 multiple fibres with four possibilities for their multiplicity: , , , and , and , , , and 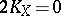, respectively.

An elliptic surface with 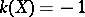is ruled (cf. Ruled surface). It is characterized by the condition 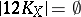. Here two cases are possible: 1) 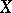is a surface with 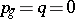, , 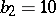and 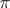has no multiple fibres or one; moreover, a surface without multiple fibres can be obtained as follows: one has to take a rational mapping 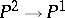determined by two cubics 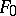and 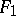and blow up their 9 points of intersection; or 2) 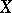is a surface with 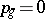, , 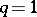, 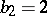and the multiplicities 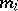are subject to the inequality

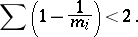The formula for the canonical class and the classification of elliptic surfaces can also be generalized to the case of a field of finite characteristic [5], [6].

The classification of non-algebraic elliptic surfaces.

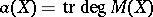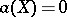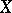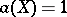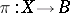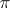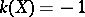
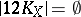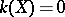
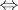
The classification of non-algebraic elliptic surfaces. For non-algebraic surfaces the algebraic dimension is 1 or 0. If , then is non-elliptic. All surfaces with are elliptic. Here the structure of is determined almost canonically: Every such fibration is necessarily elliptic. The classification by the canonical dimension is precisely the same as for algebraic elliptic surfaces: ; ; 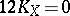and ( 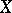is of basic type) , .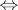

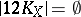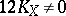Non-algebraic elliptic surfaces with 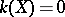belong to one of the following classes: 1) the 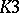-surfaces (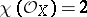, , 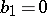, 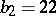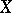is simply connected); 2) the complex tori (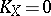, , 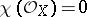, 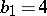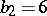); 3) the Kodaira surfaces (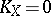, , 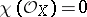, 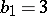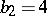). Primary Kodaira surfaces are holomorphically locally trivial fibrations over an elliptic curve with an elliptic curve as typical fibre, and from the point of view of differentiability, bundles over a -dimensional torus with a circle as fibre; or 4) the surfaces with 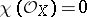, , 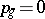, 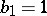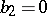. For them 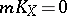with 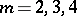, (analogous to hyper-elliptic surfaces). They have Kodaira surfaces as finite unramified coverings. In the cases 2), 3) and 4) 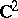is the universal covering of .

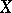Non-algebraic elliptic surfaces with 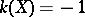are Hopf surfaces, that is, their universal covering is 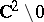. For them 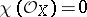, , 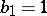. The proper Hopf surfaces are 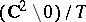, where 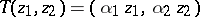are real generators of 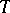. They are homeomorphic to 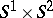and are characterized by this property. Arbitrary elliptic Hopf surfaces are quotients of proper Hopf surfaces .

References

[1]	"Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965)
[2]	D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1982) pp. 329–420
[3a]	K. Kodaira, "On compact complex analytic surfaces I" Ann. of Math. (2) , 71 (10) pp. 111–152
[3b]	K. Kodaira, "On compact complex analytic surfaces II" Ann. of Math. (2) , 77 (1963) pp. 563–626
[3c]	K. Kodaira, "On compact complex analytic surfaces III" Ann. of Math. (2) , 78 (1963) pp. 1–40
[4a]	K. Kodaira, "On the structure of compact complex analytic surfaces I" Amer. J. Math. , 86 (1964) pp. 751–798
[4b]	K. Kodaira, "On the structure of compact complex analytic surfaces II" Amer. J. Math. , 88 (1966) pp. 682–721
[4c]	K. Kodaira, "On the structure of compact complex analytic surfaces III" Amer. J. Math. , 90 (1968) pp. 55–83
[4d]	K. Kodaira, "On the structure of compact complex analytic surfaces IV" Amer. J. Math. , 90 (1968) pp. 1048–1066
[5]	D. Mumford, "Enriques' classification of surfaces in char 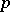. I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Princeton Univ. Press (1969) pp. 325–339
[6]	E. Bombieri, D. Mumford, "Enriques' classification of surfaces in char 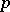. II" W.L. Baily jr. (ed.) T. Shioda (ed.) , Complex Analysis and Algebraic geometry , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42

Comments

A secondary Kodaira surface is a surface other than a primary one, admitting a primary Kodaira surface as an unramified covering. They are elliptic fibrations over a rational curve. Their first Betti number is 1.

The canonical dimension 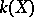mentioned at the start of the section on classification of algebraic elliptic surfaces is the Kodaira dimension 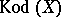(with if ).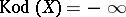

References

[a1]	W. Barth, C. Peters, A. van der Ven, "Compact complex surfaces" , Springer (1984)